
【题目】如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD,CD于G,F两点.若M,N分别是DG,CE的中点,则MN的长为( )

A. 3 B. 4 C. ![]() D.
D. ![]()
【答案】D
【解析】分析:作辅助线,构建全等三角形,证明△EMF≌△CMD,则EM=CM,利用勾股定理得:BD=![]() ,EC=
,EC=![]() ,可得△EBG是等腰直角三角形,分别求EM=CM的长,利用勾股定理的逆定理可得△EMC是等腰直角三角形,根据直角三角形斜边中线的性质得MN的长.
,可得△EBG是等腰直角三角形,分别求EM=CM的长,利用勾股定理的逆定理可得△EMC是等腰直角三角形,根据直角三角形斜边中线的性质得MN的长.
详解:连接FM、EM、CM,
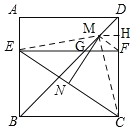
∵四边形ABCD为正方形,
∴∠ABC=∠BCD=∠ADC=90°,BC=CD,
∵EF∥BC,
∴∠GFD=∠BCD=90°,EF=BC,
∴EF=BC=DC,
∵∠BDC=![]() ∠ADC=45°,
∠ADC=45°,
∴△GFD是等腰直角三角形,
∵M是DG的中点,
∴FM=DM=MG,FM⊥DG,
∴∠GFM=∠CDM=45°,
∴△EMF≌△CMD,
∴EM=CM,
过M作MH⊥CD于H,
由勾股定理得:BD=![]() ,
,
EC=![]() ,
,
∵∠EBG=45°,
∴△EBG是等腰直角三角形,
∴EG=BE=4,
∴BG=4![]() ,
,
∴DM=![]() ,
,
∴MH=DH=1,
∴CH=61=5,
∴CM=EM=![]() ,
,
∵CE2=EM2+CM2,
∴∠EMC=90°,
∵N是EC的中点,
∴MN=![]() EC=
EC=![]() ;
;
故选:D.


科目:初中数学 来源: 题型:
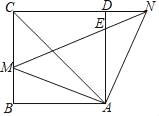
【题目】如图,在正方形ABCD中,点M是边BC上的一点(不与B、C重合),点N在CD边的延长线上,且满足∠MAN=90°,联结MN、AC,N与边AD交于点E.
(1)求证:AM=AN;
(2)如果∠CAD=2∠NAD,求证:AM2=ACAE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() ,以
,以![]() 为边在数轴的上方作正方形ABCD.动点
为边在数轴的上方作正方形ABCD.动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿数轴正方向匀速运动,同时动点
个单位长度的速度沿数轴正方向匀速运动,同时动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 匀速运动,到达
匀速运动,到达![]() 点后再以同样的速度沿数轴正方向匀速运动,设运动时间为
点后再以同样的速度沿数轴正方向匀速运动,设运动时间为![]() 秒
秒![]() .
.
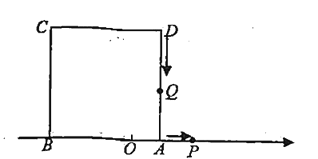
(1)若点![]() 在线段
在线段![]() .上运动,当t为何值时,
.上运动,当t为何值时,![]() ?
?
(2)若点![]() 在线段
在线段![]() 上运动,连接
上运动,连接![]() ,当t为何值时,三角形
,当t为何值时,三角形![]() 的面积等于正方形
的面积等于正方形![]() 面积的
面积的![]() ?
?
(3)在点![]() 和点
和点![]() 运动的过程中,当
运动的过程中,当![]() 为何值时,点
为何值时,点![]() 与点
与点![]() 恰好重合?
恰好重合?
(4)当点![]() 在数轴上运动时,是否存在某-时刻t,使得线段
在数轴上运动时,是否存在某-时刻t,使得线段![]() 的长为
的长为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在综合与实践课上,老师组织同学们以“矩形纸片的折叠”为主题开展数学活动.
(1)奋进小组用图1中的矩形纸片ABCD,按照如图2所示的方式,将矩形纸片沿对角线AC折叠,使点B落在点![]() 处,则
处,则![]() 与
与![]() 重合部分的三角形的类型是________.
重合部分的三角形的类型是________.
(2)勤学小组将图2中的纸片展平,再次折叠,如图3,使点A与点C重合,折痕为EF,然后展平,则以点A、F、C、E为顶点的四边形是什么特殊四边形?请说明理由.
(3)创新小组用图4中的矩形纸片ABCD进行操作,其中![]() ,
,![]() ,先沿对角线BD对折,点C落在点
,先沿对角线BD对折,点C落在点![]() 的位置,
的位置,![]() 交AD于点G,再按照如图5所示的方式折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M.则EM的长为________cm.
交AD于点G,再按照如图5所示的方式折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M.则EM的长为________cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电动车厂一周计划生产2100辆电动车,平均每天计划生产300辆,由于各种原因,实际每天的生产量与计划量相比有出入.下表是某周的生产情况(超产为正,减产为负).
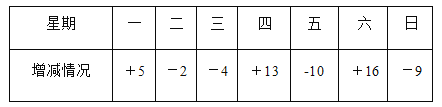
(1)根据记录可知本周前三天共生产电动车多少辆?
(2)本周产量最多的一天比产量最少的一天多生产电动车多少辆?
(3)该厂实行每周计件工资制,每生产一辆电动车可得a元,若超额完成,则超额部分每辆再奖b元(b<a),少生产一辆扣b元,求该厂工人这一周的工资总额.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①②所示,将两个相同三角板的两个直角顶点O重合在一起.

(1)若![]() ,如图①,请求出
,如图①,请求出![]() 的度数;
的度数;
(2)若![]() ,如图②,请求出
,如图②,请求出![]() 的度数;
的度数;
(3)猜想:![]() 和
和![]() 的关系(请直接写出答案即可)
的关系(请直接写出答案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中:
①在Rt△ABC中,∠C=90°,CD为AB边上的中线,若CD=2,则AB=4;
②八边形的内角和度数为1080°;
③2、3、4、3这组数据的方差为0.5;
④分式方程![]() =
=![]() 的解为x=
的解为x=![]() ;
;
⑤已知菱形的一个内角为60°,一条对角线为2,则另一对角线为2![]() .
.
正确的序号有( )
A. ①②③⑤ B. ①②③④ C. ①③④⑤ D. ②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图直线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]()
(1)图中与![]() 互余的角有 ,图中与
互余的角有 ,图中与![]() 互补的角有 (备注:写出所有符合条件的角)
互补的角有 (备注:写出所有符合条件的角)
(2)根据下列条件,分别求![]() 的度数:①射线
的度数:①射线![]() 平分
平分![]() ;②
;②![]()
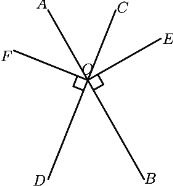
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com