
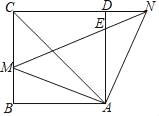
【题目】如图,在正方形ABCD中,点M是边BC上的一点(不与B、C重合),点N在CD边的延长线上,且满足∠MAN=90°,联结MN、AC,N与边AD交于点E.
(1)求证:AM=AN;
(2)如果∠CAD=2∠NAD,求证:AM2=ACAE.
【答案】(1)证明见解析;(2)证明见解析.
【解析】分析:(1)根据正方形的性质、全等三角形的判定定理证明△BAM≌△DAN,根据全等三角形的性质证明;
(2)证明△AMC∽△AEN,根据相似三角形的性质证明.
详解:(1)∵四边形ABCD是正方形,∴ AB=AD,∠BAD=90°,
又∵∠MAN=90°,∴∠BAM=∠DAN.
在△BAM和△DAN中,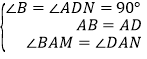 ,
,
∴△BAM≌△DAN,∴AM=AN;
(2)四边形ABCD是正方形,∴∠CAD=45°.
∵∠CAD=2∠NAD,∠BAM=∠DAN,
∴∠MAC=45°,∴∠MAC=∠EAN,
又∠ACM=∠ANE=45°,∴△AMC∽△AEN,
∴![]() =
=![]() ,∴ANAM=ACAE,∴AM2=ACAE.
,∴ANAM=ACAE,∴AM2=ACAE.


科目:初中数学 来源: 题型:
【题目】火车匀速通过隧道时,火车在隧道内的长度![]() (米)与火车行驶时间
(米)与火车行驶时间![]() (秒)之间的关系用图象描述如图所示,有下列结论:
(秒)之间的关系用图象描述如图所示,有下列结论:
①火车的长度为120米;
②火车的速度为30米/秒;
③火车整体都在隧道内的时间为25秒;
④隧道长度为750米.
其中正确的结论是_____.(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中有一小岛P,在距小岛P的![]() 海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?
海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA的方向是北偏东15°,OB的方向是西偏北50°,OD是OB的反向延长线.

(1)若∠AOC=∠AOB,求OC的方向.
(2)在(1)问的条件下,作∠AOD的角平分线OE,求∠COE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图,用同样规格的黑白两色正方形瓷砖铺设矩形地面,请观察图形,并探究下列问题:
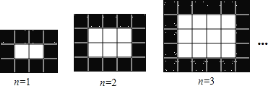
![]() 在第
在第![]() 个图中,共有白色瓷砖________块;在第
个图中,共有白色瓷砖________块;在第![]() 个图中,共有白色瓷砖________块;
个图中,共有白色瓷砖________块;
![]() 在第
在第![]() 个图中,共有瓷砖________块;在第
个图中,共有瓷砖________块;在第![]() 个图中,共有瓷砖________块;
个图中,共有瓷砖________块;
![]() 如果每块黑瓷砖
如果每块黑瓷砖![]() 元,白瓷砖
元,白瓷砖![]() 元,铺设当
元,铺设当![]() 时,共需花多少钱购买瓷砖?
时,共需花多少钱购买瓷砖?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明遇到这样一个问题,如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC.求∠C的度数。小明通过探究发现,延长CD至点Q,使BQ=AB,再证明△ADC≌△ADQ,使问题得到解决.

(1)根据阅读材料回答,△ADC≌△ADQ的条件是________(填SSS,SAS,AAS,ASA,或HL)
(2)参考小明思考问题的方法,解答下列问题:求∠C的度数;
(3)解决问题,如图,已知,△ABC中,过点B任意作射线l,在l上取一点D,使∠ABD=∠ACD,AM⊥BD于点M,且BM=MD+CD。探究AB与AC的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD,AB=6,AD=8,将矩形ABCD绕点A顺时针旋转θ(0°<θ<360°)得到矩形AEFG,当θ=_____°时,GC=GB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】节约是中华民族的传统美德.为倡导市民节约用水的意识,某市对市民用水实行“阶梯收费”,制定了如下用水收费标准:每户每月的用水不超过![]() 立方米时,水价为每立方米
立方米时,水价为每立方米![]() 元,超过
元,超过![]() 立方米时,超过的部分按每立方米
立方米时,超过的部分按每立方米![]() 元收费.
元收费.
(1)该市某户居民9月份用水![]() 立方米(
立方米(![]() ),应交水费
),应交水费![]() 元,请你用含
元,请你用含![]() 的代数式表示
的代数式表示![]() ;
;
(2)如果某户居民12月份交水费![]() 元,那么这个月该户居民用了多少立方米水?
元,那么这个月该户居民用了多少立方米水?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD,CD于G,F两点.若M,N分别是DG,CE的中点,则MN的长为( )

A. 3 B. 4 C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com