
【题目】小明遇到这样一个问题,如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC.求∠C的度数。小明通过探究发现,延长CD至点Q,使BQ=AB,再证明△ADC≌△ADQ,使问题得到解决.

(1)根据阅读材料回答,△ADC≌△ADQ的条件是________(填SSS,SAS,AAS,ASA,或HL)
(2)参考小明思考问题的方法,解答下列问题:求∠C的度数;
(3)解决问题,如图,已知,△ABC中,过点B任意作射线l,在l上取一点D,使∠ABD=∠ACD,AM⊥BD于点M,且BM=MD+CD。探究AB与AC的数量关系,并证明.

【答案】(1)证明见解析;(2)∠C=20°;(3)AB=AC,理由见解析.
【解析】
(1)根据SAS即可证明;
(2)根据△ADQ≌△ADC,推出∠ABC=2∠Q=2∠C,即可解决问题;
(3)如图,在MB上截取MH=DM,连接AH、AD,作HF⊥AB于F,作DE⊥AC于E,先证明△BHF≌△CDE,推出HF=DE,由AH=AD,推出Rt△AHF≌Rt△ADE,推出∠BAH=∠CAD,由∠ABH=∠ACD,BH=CD,再证明△ABH≌△ACD即可解决问题.
(1)如图,延长CD至点Q,使BQ=AB,

∵AD⊥BC于D,
∴∠ADC=∠ADQ=90°,
∵AB+BD=CD,AB=BQ,
∴BD+BQ=DQ=DC,
∵AD=AD,
∴△ADQ≌△ADC(SAS),
∴△ADC≌△ADQ的理由是(SAS);
(2)∵△ADQ≌△ADC
∴∠Q=∠C,
∵BA=BQ,
∴∠Q=∠BAQ,
∵∠ABC=∠Q+∠BAQ,
∴∠ABC=2∠C,
∵∠BAC=120°,
∴3∠C=60°,
∴∠C=20°;
(3)AB=AC,
理由:如图,在MB上截取MH=DM,连接AH、AD.作HF⊥AB于F,作DE⊥AC于E.

∵AM⊥DH,MH=MD,
∴AH=AD,
∵BM=DM+DC=BH+MH,
∵CD=BH,
∵∠DEC=∠HFB=90°,∠HBF=∠DCE,
∴△BHF≌△CDE,
∴HF=DE,
∵AH=AD,
∴Rt△AHF≌Rt△ADE,
∴∠BAH=∠CAD,
∵∠ABH=∠ACD,BH=CD,
∴△ABH≌△ACD,
∴AB=AC.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
【题目】中考体育测试前,某区教育局为了了解选报引体向上的初三男生的成绩情况,随机抽测了本区部分选报引体向上项目的初三男生的成绩,并将测试得到的成绩绘成了下面两幅不完整的统计图:
请你根据图中的信息,解答下列问题:
(![]() )写出扇形图中
)写出扇形图中![]() __________
__________![]() ,并补全条形图.
,并补全条形图.
(![]() )在这次抽测中,测试成绩的众数和中位数分别是__________个、__________个.
)在这次抽测中,测试成绩的众数和中位数分别是__________个、__________个.
(![]() )该区体育中考选报引体向上的男生共有
)该区体育中考选报引体向上的男生共有![]() 人,如果体育中考引体向上达
人,如果体育中考引体向上达![]() 个以上(含
个以上(含![]() 个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名?
个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面由※组成的图案和算式,解答问题:

![]()
![]()
![]()
![]()
(1)请猜想![]() ____= ______;
____= ______;
(2)请猜想![]() _________;
_________;
(3)请用上述规律计算:![]() 的值;
的值;
(4)请用上述规律计算: ![]() ______(直接写答案).
______(直接写答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)探究:哪些特殊的角可以用一副三角板画出?
在①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 中,小明同学利用一副三角板画不出来的特殊角是_________;(填序号)
中,小明同学利用一副三角板画不出来的特殊角是_________;(填序号)
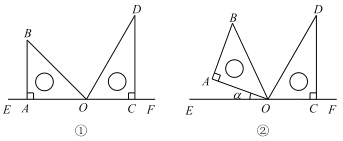
(2)在探究过程中,爱动脑筋的小明想起了图形的运动方式有多种.如图,他先用三角板画出了直线![]() ,然后将一副三角板拼接在一起,其中
,然后将一副三角板拼接在一起,其中![]() 角(
角(![]() )的顶点与
)的顶点与![]() 角(
角(![]() )的顶点互相重合,且边
)的顶点互相重合,且边![]() 、
、![]() 都在直线
都在直线![]() 上.固定三角板
上.固定三角板![]() 不动,将三角板
不动,将三角板![]() 绕点
绕点![]() 按顺时针方向旋转一个角度
按顺时针方向旋转一个角度![]() ,当边
,当边![]() 与射线
与射线![]() 第一次重合时停止.
第一次重合时停止.
①当![]() 平分
平分![]() 时,求旋转角度
时,求旋转角度![]() ;
;
②是否存在![]() ?若存在,求旋转角度
?若存在,求旋转角度![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
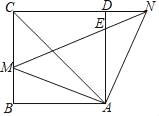
【题目】如图,在正方形ABCD中,点M是边BC上的一点(不与B、C重合),点N在CD边的延长线上,且满足∠MAN=90°,联结MN、AC,N与边AD交于点E.
(1)求证:AM=AN;
(2)如果∠CAD=2∠NAD,求证:AM2=ACAE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划开设四门选修课:乐器、舞蹈、绘画、书法.为提前了解学生的选修情况,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行了整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:

(1)本次调查的学生共有 人,在扇形统计图中,m的值是 ;
(2)将条形统计图补充完整;
(3)在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请直接写出所抽取的2名同学恰好是1名男同学和1名女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为打造美丽校园,小明、小红为校园内的一块空地分别提供了如图甲、乙的设计方案,其中阴影部分都用于绿化,图甲空白区域修建一座雕像,图乙空白区域修建石子小路.已知S甲表示图甲中绿化的面积S乙表示图乙中绿化的面积.
(1)S甲= (用含a,b的代数式表示);
(2)设k=![]() ,
,
①请用含a,b的代数式表示k并化简;
②当2S甲﹣S乙=![]() a2时,求k的值.
a2时,求k的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:
某校要举办足球赛,若有5支球队进行单循环比赛(即全部比赛过程中任何一队都要分别与其他各队比赛一场且只比赛一场),则该校一共要安排多少场比赛?
构建模型:
生活中的许多实际问题,往往需要构建相应的数学模型,利用模型的思想来解决问题.
为解决上述问题,我们构建如下数学模型:
(1)如图①,我们可以在平面内画出5个点(任意3个点都不在同一条直线上),其中每个点各代表一支足球队,两支球队之间比赛一场就用一条线段把他们连接起来.由于每支球队都要与其他各队比赛一场,即每个点与另外4个点都可连成一条线段,这样一共连成5×4条线段,而每两个点之间的线段都重复计算了一次,实际只有 条线段,所以该校一共要安排 场比赛.

(2)若学校有6支足球队进行单循环比赛,借助图②,我们可知该校一共要安排__________场比赛;
…………
(3)根据以上规律,若学校有n支足球队进行单循环比赛,则该校一共要安排___________场比赛.
实际应用:
(4)9月1日开学时,老师为了让全班新同学互相认识,请班上42位新同学每两个人都相互握一次手,全班同学总共握手________________次.
拓展提高:
(5)往返于青岛和济南的同一辆高速列车,中途经青岛北站、潍坊、青州、淄博4个车站(每种车票票面都印有上车站名称与下车站名称),那么在这段线路上往返行车,要准备车票的种数为__________种.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①②所示,将两个相同三角板的两个直角顶点O重合在一起.

(1)若![]() ,如图①,请求出
,如图①,请求出![]() 的度数;
的度数;
(2)若![]() ,如图②,请求出
,如图②,请求出![]() 的度数;
的度数;
(3)猜想:![]() 和
和![]() 的关系(请直接写出答案即可)
的关系(请直接写出答案即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com