
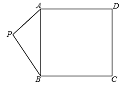
【题目】如图,已知P是正方形ABCD外一点,且PA=3,PB=4 ,则PC的最大值是________;
【答案】![]()
【解析】分析:过点B作BE⊥BP使点E在正方形ABCD的外部,且BE=PB,连接AE、PE、PC,然后求出PE=![]() PB,再求出∠ABE=∠CBP,然后利用“边角边”证明△ABE和△CBP全等,根据全等三角形对应边相等可得AE=PC,再根据两点之间线段最短可知点A、P、E三点共线时AE最大,也就是PC最大.
PB,再求出∠ABE=∠CBP,然后利用“边角边”证明△ABE和△CBP全等,根据全等三角形对应边相等可得AE=PC,再根据两点之间线段最短可知点A、P、E三点共线时AE最大,也就是PC最大.
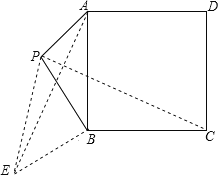
详解:如图,过点B作BE⊥BP,且BE=PB,连接AE、PE、PC,
则PE=![]() PB=4
PB=4![]() ,
,
∵∠ABE=∠ABP+90,∠CBP=∠ABP+90,
∴∠ABE=∠CBP,
在△ABE和△CBP中,
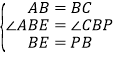 ,
,
∴△ABE≌△CBP(SAS),
∴AE=PC,
由两点之间线段最短可知,点A. P、E三点共线时AE最大,
此时AE=AP+PE=3+4![]() ,
,
所以,PC的最大值是3+4![]() .
.
故答案为:3+4![]() .
.


科目:初中数学 来源: 题型:
【题目】已知矩形ABCD,AB=6,AD=8,将矩形ABCD绕点A顺时针旋转θ(0°<θ<360°)得到矩形AEFG,当θ=_____°时,GC=GB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD,CD于G,F两点.若M,N分别是DG,CE的中点,则MN的长为( )

A. 3 B. 4 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李老师准备购买一套小户型商品房,他去售楼处了解情况得知.该户型商品房的单价是5000元/![]() ,面积如图所示(单位:m,卫生间的宽未定,设宽为xm),售房部为李老师提供了以下两种优惠方案:
,面积如图所示(单位:m,卫生间的宽未定,设宽为xm),售房部为李老师提供了以下两种优惠方案:
方案一:整套房的单价为5000元/![]() ,其中厨房可免费赠送一半的面积;
,其中厨房可免费赠送一半的面积;
方案二:整套房按原销售总金额的9.5折出售.

(1)用含x的代数式表示该户型商品房的面积及方案一、方案二中购买一套该户型商品房的总金额;
(2)当x=2时,通过计算说明哪种方案更优惠?优惠多少元?
(3)李老师因现金不够,于2019年10月在建行借了18万元住房贷款,贷款期限为10年,从开始贷款的下一个月起逐月偿还,贷款月利率是0.5%,每月应还的贷款本金数额为1500元(每月还款数额=每月应还的贷款本金数额+月利息,月利息=上月所剩贷款本金数额×月利率),假设贷款月利率不变,请求出李老师在借款后第n(![]() ,n是正整数)个月的还款数额.(用n的代数式表示)
,n是正整数)个月的还款数额.(用n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
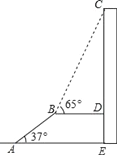
【题目】如图,AB是长为10m,倾斜角为37°的自动扶梯,平台BD与大楼CE垂直,且与扶梯AB的长度相等,在B处测得大楼顶部C的仰角为65°,求大楼CE的高度(结果保留整数).
(参考数据:sin37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin65°≈
,sin65°≈![]() ,tan65°≈
,tan65°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.

(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
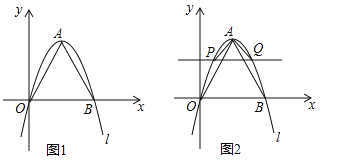
【题目】(2016吉林省)如图1,在平面直角坐标系中,点B在x轴正半轴上,OB的长度为2m,以OB为边向上作等边三角形AOB,抛物线l:![]() 经过点O,A,B三点.
经过点O,A,B三点.
(1)当m=2时,a= ,当m=3时,a= ;
(2)根据(1)中的结果,猜想a与m的关系,并证明你的结论;
(3)如图2,在图1的基础上,作x轴的平行线交抛物线l于P、Q两点,PQ的长度为2n,当△APQ为等腰直角三角形时,a和n的关系式为 ;
(4)利用(2)(3)中的结论,求△AOB与△APQ的面积比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】珠江流域某江段江水流向经过B、C、D三点拐弯后与原来相同,如图,若∠ABC=120°,∠BCD=80°,则∠CDE=__________度.

(第22题)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com