
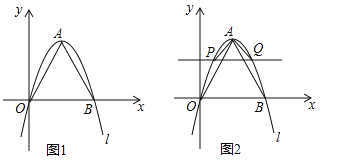
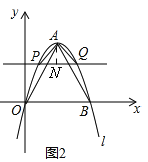
����Ŀ����2016����ʡ����ͼ1����ƽ��ֱ������ϵ�У���B��x���������ϣ�OB�ij���Ϊ2m����OBΪ���������ȱ�������AOB��������l��![]() ������O��A��B���㣮
������O��A��B���㣮
��1����m=2ʱ��a= ����m=3ʱ��a= ��
��2�����ݣ�1���еĽ��������a��m�Ĺ�ϵ����֤����Ľ��ۣ�
��3����ͼ2����ͼ1�Ļ����ϣ���x���ƽ���߽�������l��P��Q���㣬PQ�ij���Ϊ2n������APQΪ����ֱ��������ʱ��a��n�Ĺ�ϵʽΪ ��
��4�����ã�2����3���еĽ��ۣ�����AOB����APQ������ȣ�
���𰸡���1��![]() ��
��![]() ����2��
����2��![]() ����3��
����3��![]() ����4��
����4��![]() ��1��
��1��
�������������������1������AOBΪ�ȱ������Σ�AB=2m���ó���A��B���꣬���ɵ�A��B��O���������Ͻ��������飬�ó����ۣ�����m=2��m=3����ֵ���ɣ�
��2��ͬ��1���ķ����ó�����
��3������APQΪ����ֱ�������Σ�PQ�ij���Ϊ2n����A��e��d+n������P��e��n��d����Q��e+n��d����������������⼴�ɣ�
��4���ɣ�2����3���Ľ��۵õ�m=![]() n���ٸ��������ʽ�г�ʽ�ӣ����뻯�ɣ�
n���ٸ��������ʽ�г�ʽ�ӣ����뻯�ɣ�
����������⣺��1����ͼ1������B��x���������ϣ�OB�ij���Ϊ2m����B��2m��0��������OBΪ���������ȱ�������AOB����AM=![]() m��OM=m����A��m��
m��OM=m����A��m��![]() m������������l��
m������������l��![]() ������O��A��B��������
������O��A��B��������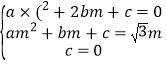 ����
����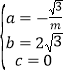 ��
��
��m=2ʱ��a=![]() ����m=3ʱ��a=
����m=3ʱ��a=![]() ���ʴ�Ϊ��
���ʴ�Ϊ��![]() ��
��![]() ��
��
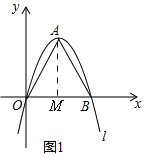
��2��![]() �����ɣ���ͼ1������B��x���������ϣ�OB�ij���Ϊ2m����B��2m��0��������OBΪ���������ȱ�������AOB����AM=
�����ɣ���ͼ1������B��x���������ϣ�OB�ij���Ϊ2m����B��2m��0��������OBΪ���������ȱ�������AOB����AM=![]() m��OM=m����A��m��
m��OM=m����A��m��![]() m������������l��
m������������l��![]() ������O��A��B��������
������O��A��B��������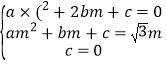 ����
����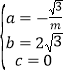 ����
����![]() ��
��
��3����ͼ2���ߡ�APQΪ����ֱ�������Σ�PQ�ij���Ϊ2n����A��e��d+n������P��e��n��d����Q��e+n��d������P��Q��A��O��������l��![]() �ϣ���
�ϣ���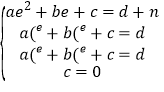 ����
����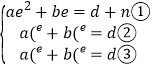 ���٩�������ã�2ae��an+b=1�ܣ��٩������������2ae��an��b=1�ݣ���+���������an=��1����
���٩�������ã�2ae��an+b=1�ܣ��٩������������2ae��an��b=1�ݣ���+���������an=��1����![]() ���ʴ�Ϊ��
���ʴ�Ϊ��![]() ��
��
��4����OB�ij���Ϊ2m��AM=![]() m����S��AOB=
m����S��AOB=![]() OB��AM=
OB��AM=![]() ��2m��
��2m��![]() m=
m=![]() ���ɣ�3���У�AN=n��
���ɣ�3���У�AN=n��
��PQ�ij���Ϊ2n����S��APQ=![]() PQ��AN=
PQ��AN=![]() ��2n��n=
��2n��n=![]() ���ɣ�2����3���У�
���ɣ�2����3���У�![]() ��
��![]() ����
����![]() ����m=
����m=![]() n����
n����![]() =
=![]() =
=![]() =
=![]() �����AOB����APQ�������Ϊ
�����AOB����APQ�������Ϊ![]() ��1��
��1��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�����ϵ�![]() ��ʾ����Ϊ
��ʾ����Ϊ![]() ,��
,��![]() ��ʾ����Ϊ
��ʾ����Ϊ![]() ,��
,��![]() Ϊ����������Ϸ���������ABCD.����
Ϊ����������Ϸ���������ABCD.����![]() �ӵ�
�ӵ�![]() ����,��ÿ��
����,��ÿ��![]() ����λ���ȵ��ٶ������������������˶���ͬʱ����
����λ���ȵ��ٶ������������������˶���ͬʱ����![]() �ӵ�
�ӵ�![]() ����,��ÿ��
����,��ÿ��![]() ����λ���ȵ��ٶ����
����λ���ȵ��ٶ����![]() �����˶�������
�����˶�������![]() �������ͬ�����ٶ������������������˶������˶�ʱ��Ϊ
�������ͬ�����ٶ������������������˶������˶�ʱ��Ϊ![]() ��
��![]() .
.
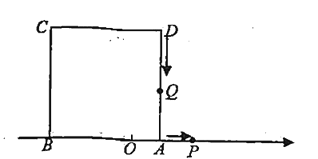
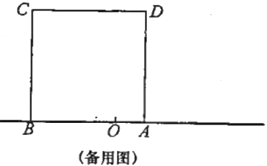
(1)����![]() ���߶�
���߶�![]() .���˶�����tΪ��ֵʱ,
.���˶�����tΪ��ֵʱ,![]() ?
?
(2)����![]() ���߶�
���߶�![]() ���˶�������
���˶�������![]() ,��tΪ��ֵʱ,������
,��tΪ��ֵʱ,������![]() ���������������
���������������![]() �����
�����![]() ?
?
(3)�ڵ�![]() �͵�
�͵�![]() �˶��Ĺ����У���
�˶��Ĺ����У���![]() Ϊ��ֵʱ����
Ϊ��ֵʱ����![]() ���
���![]() ǡ���غ�?
ǡ���غ�?
(4)����![]() ���������˶�ʱ���Ƿ����ij-ʱ��t,ʹ���߶�
���������˶�ʱ���Ƿ����ij-ʱ��t,ʹ���߶�![]() �ij�Ϊ
�ij�Ϊ![]() ,�����ڣ����
,�����ڣ����![]() ��ֵ;�������ڣ���˵������.
��ֵ;�������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
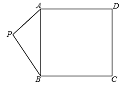
����Ŀ����ͼ,��֪P��������ABCD��һ��,��PA=3,PB=4 ,��PC�����ֵ��________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���У�
����Rt��ABC�У���C=90�㣬CDΪAB���ϵ����ߣ���CD=2����AB=4��
�ڰ˱��ε��ڽǺͶ���Ϊ1080�㣻
��2��3��4��3�������ݵķ���Ϊ0.5��
�ܷ�ʽ����![]() =
=![]() �Ľ�Ϊx=
�Ľ�Ϊx=![]() ��
��
����֪���ε�һ���ڽ�Ϊ60����һ���Խ���Ϊ2������һ�Խ���Ϊ2![]() ��
��
��ȷ������У� ��
A. �٢ڢۢ� B. �٢ڢۢ� C. �٢ۢܢ� D. �ڢۢܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У���E��F�ֱ��ڱ�AB��CD�ϣ���G��H�ڶԽ���AC�ϣ�EF��AC�ཻ�ڵ�O��AG=CH��BE=DF��
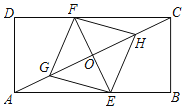
��1����֤���ı���EGFH��ƽ���ı��Σ�
��2����EG=EHʱ������AF
����֤��AF=FC��
����DC=8��AD=4����AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ijͬѧ�Զ���ʽ��x2��4x+2����x2��4x+6��+4������ʽ�ֽ�Ĺ��̣�
�⣺��x2��4x=y
ԭʽ=��y+2����y+6��+4 ����һ����
= y2+8y+16 ���ڶ�����
=��y+4��2 ����������
=��x2��4x+4��2 �����IJ���
�ش��������⣺
��1����ͬѧ�ڶ�������������������ʽ�ֽ��_______��
A����ȡ����ʽ B��ƽ���ʽ C�������͵���ȫƽ����ʽ D�����������ȫƽ����ʽ
��2����ͬѧ��ʽ�ֽ�Ľ���Ƿף�________��������ס������ס���
�������ף���ֱ��д����ʽ�ֽ�������_________��
��3������ģ�����Ϸ������ԶԶ���ʽ��x2��2x����x2��2x+2��+1������ʽ�ֽ⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ժ�Ĺ���ϯ����λΪ���Σ��Ұ����з�ʽ���ã�
������x�� | 1 | 2 | 3 | 4 | �� |
�����y�� | 50 | 53 | 56 | 59 | �� |
��1�������ϱ���ʾ�Ĺ��ɣ���xÿ����1ʱ��y��α仯��
��2��д����λ��y������x֮��Ĺ�ϵʽ��
��3�������ϱ���ʾ�Ĺ��ɣ�ijһ�ſ�����90����λ��˵˵������ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
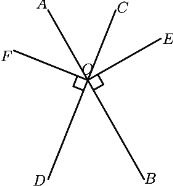
����Ŀ����֪����ͼֱ��![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��![]()
��1��ͼ����![]() ����Ľ��� ��ͼ����
����Ľ��� ��ͼ����![]() �����Ľ��� ����ע��д�����з��������Ľǣ�
�����Ľ��� ����ע��д�����з��������Ľǣ�
��2�����������������ֱ���![]() �Ķ�����������
�Ķ�����������![]() ƽ��
ƽ��![]() ����
����![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
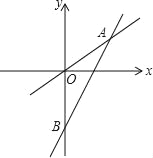
����Ŀ����ͼ��ʾһ��������������һ��һ�κ�����ͼ�����ǽ��ڵ�A��4��3����һ�κ�����ͼ����y�ύ�ڵ�B����OA=OB��
��1���������������Ľ���ʽ��
��2������OAB�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com