
����Ŀ������ʦ������һ��С������Ʒ������ȥ��¥���˽������֪���û�����Ʒ���ĵ�����5000Ԫ/![]() �������ͼ��ʾ(��λ��m��������Ŀ�δ�������Ϊxm)���۷���Ϊ����ʦ�ṩ�����������Żݷ�����
�������ͼ��ʾ(��λ��m��������Ŀ�δ�������Ϊxm)���۷���Ϊ����ʦ�ṩ�����������Żݷ�����
����һ�������ĵ���Ϊ5000Ԫ/![]() �����г������������һ��������
�����г������������һ��������
��������������ԭ�����ܽ���9.5�۳��ۣ�

��1���ú�x�Ĵ���ʽ��ʾ�û�����Ʒ�������������һ���������й���һ�û�����Ʒ�����ܽ�
��2����x=2ʱ��ͨ������˵�����ַ������Żݣ��Żݶ���Ԫ��
��3������ʦ���ֽ�����2019��10���ڽ��н���18��Ԫס�������������Ϊ10�꣬�ӿ�ʼ�������һ���������³�����������������0.5%��ÿ��Ӧ���Ĵ��������Ϊ1500Ԫ(ÿ�»�������=ÿ��Ӧ���Ĵ��������+����Ϣ������Ϣ=������ʣ�����������������)��������������ʲ��䣬���������ʦ�ڽ����n(![]() ��n��������)���µĻ������(��n�Ĵ���ʽ��ʾ)
��n��������)���µĻ������(��n�Ĵ���ʽ��ʾ)
���𰸡���1���û�����Ʒ�������Ϊ(48+2x)ƽ���ף�����һ��(![]() )Ԫ����������(
)Ԫ����������(![]() )Ԫ����2������һ�ȷ������Ż�7000Ԫ����3��(
)Ԫ����2������һ�ȷ������Ż�7000Ԫ����3��(![]() )Ԫ��
)Ԫ��
��������
��1���û�����Ʒ�������=���������+�������+�������+�����������������㼴�ɣ�
����һ��(�������������![]() )�����ۣ�
)�����ۣ�
������������������ۡ�95%��
��2���ֱ������㣬Ȼ��Ƚϼ��ɣ�
��3��������ã�����1500+����Ϣ��������㣮
��1���û�����Ʒ�������Ϊ��
![]() (ƽ����)
(ƽ����)
����һ����һ�û�����Ʒ�����ܽ��Ϊ��
![]() (Ԫ)
(Ԫ)
����������һ�û�����Ʒ�����ܽ��Ϊ��
![]() (Ԫ)
(Ԫ)
��2����![]() ʱ������һ�ܽ��Ϊ��
ʱ������һ�ܽ��Ϊ��![]() (Ԫ)
(Ԫ)
�������ܽ��Ϊ��![]() (Ԫ)
(Ԫ)
����һ�ȷ������Ż�7000Ԫ��
��3����������ã�����ʦ�ڽ����n(![]() ��n��������)���µĻ�������Ϊ
��n��������)���µĻ�������Ϊ
![]() (Ԫ)
(Ԫ)



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCΪֱ�������Σ���C=90�㣬BC=2cm����A=30�����ı���DEFGΪ���Σ�DE=2![]() cm��EF=6cm���ҵ�C��B��E��F��ͬһ��ֱ���ϣ���B���E�غϣ�Rt��ABC��ÿ��1cm���ٶ��ؾ���DEFG�ı�EF����ƽ�ƣ�����C���F�غ�ʱֹͣ����Rt��ABC�����DEFG���ص����ֵ����Ϊycm2���˶�ʱ��xs���ܷ�ӳycm2��xs֮�亯����ϵ�Ĵ���ͼ���ǣ�������
cm��EF=6cm���ҵ�C��B��E��F��ͬһ��ֱ���ϣ���B���E�غϣ�Rt��ABC��ÿ��1cm���ٶ��ؾ���DEFG�ı�EF����ƽ�ƣ�����C���F�غ�ʱֹͣ����Rt��ABC�����DEFG���ص����ֵ����Ϊycm2���˶�ʱ��xs���ܷ�ӳycm2��xs֮�亯����ϵ�Ĵ���ͼ���ǣ�������

A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����Rt��ABC�У���ACB��90�㣬AC��4��BC��8��O��AB�ߵ��е㣬P��AC���ϵĶ��㣬OE��OP��BC���ڵ�E������PE.
��1����ͼ�٣���P��C�غ�ʱ���߶�PE�ij�Ϊ___________��
��2����ͼ�ڣ���P��AC�����˶�ʱ��
��̽�����߶�PA��PE��EB֮���������ϵ����֤����Ľ��ۣ�
������PA=![]() ��PE2=y����y��x֮��ĺ�����ϵʽ���߶�PE����Сֵ.
��PE2=y����y��x֮��ĺ�����ϵʽ���߶�PE����Сֵ.
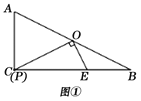
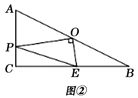
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�綯����һ�ܼƻ�����2100���綯����ƽ��ÿ��ƻ�����300�������ڸ���ԭ��ʵ��ÿ�����������ƻ�������г��룮�±���ij�ܵ��������(����Ϊ��������Ϊ��).
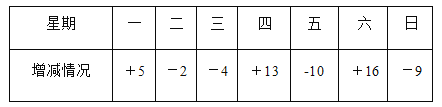
��1�����ݼ�¼��֪����ǰ���칲�����綯����������
��2�����ܲ�������һ��Ȳ������ٵ�һ��������綯����������
��3���ó�ʵ��ÿ�ܼƼ������ƣ�ÿ����һ���綯���ɵ�aԪ����������ɣ����ÿ���ٽ�bԪ(b��a)��������һ����bԪ����ó�������һ�ܵĹ����ܶ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������5��19��Ϊ��29����ȫ����������������ij��ѧ��֯���װ��ľ������У��ѧ����С��Ա��ξ������һ�γ������飬�����������²�������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ��ÿ�麬ǰһ���߽磬������һ���߽磩��

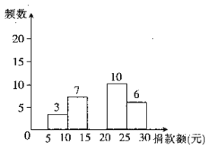
��1����գ�![]() _________��
_________��![]() _________��
_________��
��2����ȫƵ���ֲ�ֱ��ͼ��
��3����У��2000��ѧ����������λ�а��ľ�����![]() ��ѧ��������
��ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��֪P��������ABCD��һ��,��PA=3,PB=4 ,��PC�����ֵ��________��
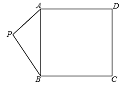
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��0��4����ֱ������ϵ y ����һ�㣬���� P ��ԭ�� O �������� x ���������˶����ٶ�Ϊÿ�� 1 ����λ���ȣ���PΪֱ�Ƕ����ڵ�һ������������Rt��APB����P����˶�ʱ��Ϊ t �룮
��1���� AB��x �ᣬ�� t ��ֵ��
��2����OP=![]() OA����B������꣮
OA����B������꣮
��3���� t=3 ʱ��x �����Ƿ������һ�� M��ʹ���� M��P��A Ϊ������������ǵ��������Σ���ֱ��д���� M �����꣮
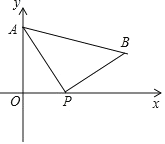
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У���E��F�ֱ��ڱ�AB��CD�ϣ���G��H�ڶԽ���AC�ϣ�EF��AC�ཻ�ڵ�O��AG=CH��BE=DF��
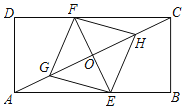
��1����֤���ı���EGFH��ƽ���ı��Σ�
��2����EG=EHʱ������AF
����֤��AF=FC��
����DC=8��AD=4����AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������y=ax2+��a+2��x+2��a��0����x�ύ�ڵ�A��4��0������y�ύ�ڵ�B����x������һ����P��m��0����0��m��4��������P��x��Ĵ��߽�ֱ��AB�ڵ�N�����������ڵ�M��

��1����a��ֵ��
��2����PN��MN=1��3����m��ֵ��
��3����ͼ2���ڣ�2���������£��趯��P��Ӧ��λ����P1�����߶�OP1�Ƶ�O��ʱ����ת�õ�OP2����ת��Ϊ����0�㣼����90����������AP2��BP2����AP2+![]() BP2����Сֵ��
BP2����Сֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com