
【题目】已知:在Rt△ABC中,∠ACB=90°,AC=4,BC=8,O是AB边的中点,P是AC边上的动点,OE⊥OP交BC边于点E,连接PE.
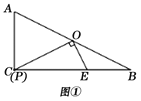
(1)如图①,当P与C重合时,线段PE的长为___________;
(2)如图②,当P在AC边上运动时,
①探究:线段PA,PE,EB之间的数量关系,并证明你的结论;
②若设PA=![]() ,PE2=y,求y与x之间的函数关系式及线段PE的最小值.
,PE2=y,求y与x之间的函数关系式及线段PE的最小值.
【答案】(1)5;(2)①PA2+EB2=PE2,证明见解析.②y=![]() x25x+25 2
x25x+25 2![]()
【解析】分析:(1)根据中线定理和直角三角形斜边上的中线分别表示出AB、OA的长度,再证明△COE∽△BCD即可.
(2)①如下图②,先判断△BOM≌△AOP,可得:BM2+EB2=ME2,又∵OE⊥PM,OM=OP,∴ME=PE,即可证明BM2+EB2=ME2.
②求出y与x之间的函数关系式即可解答.
详解:(1)在Rt△ABC中,AB=![]() ,
,
∵O是AB中点,∴OA=CO=BO=![]() AB=2
AB=2![]() .
.
∴∠OCB=∠B,又∵OE⊥OP,∴∠COE=∠A=90°.
∴△COE∽△BCD,
∴![]() ,即:
,即:![]() ,∴CE=5.
,∴CE=5.
(2)①三者的数量关系为PA2+EB2=PE2.
证明:如图②,延长PO到M,使OM=OP,连接BM,EM,

∵O是AB边的中点,∴0B=OA,
又 ∠BOM=∠AOP,∴△BOM≌△AOP,
∴∠OBM=∠OAP,BM=AP.
∴∠OBM+∠ABC=∠BAC+∠ABC=90°,
∴BM2+EB2=ME2,
又∵OE⊥PM,OM=OP,∴ME=PE,
∴PA2+EB2=PE2.
②如图②,设EB=m,则CE=8-m,∵ PA=x,则PC=4-x,又PE2=y,
在Rt△PEC中,由勾股定理得:PC2+CE2=PE2,
则(4-x)2+(8-m)2=y ①.
又PA2+EB2=PE2,则x2+m2=y,②.
由①②联解消y得:m=-![]() ③,
③,
将③代入②并整理,得:y=![]() ,
,
∴y与x之间的函数关系式为![]() ,
,
∵![]() =
=![]() ,
,
∴当x=2时,y的最小值为20,∴PE的最小值为2![]() .
.


科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,点A、B分别在函数y1=![]() (x>0),与y2=﹣
(x>0),与y2=﹣![]() (x<0)的图象上,A、B的横坐标分别为a、b.(a、b为任意实数)
(x<0)的图象上,A、B的横坐标分别为a、b.(a、b为任意实数)
(1)若AB∥x轴,求△OAB的面积;
(2)作边长为2的正方形ACDE,使AC∥x轴,点D在点A的左上方,那么,当a≥3时,CD边与函数y1=![]() (x>0)的图象有交点,请说明理由.
(x>0)的图象有交点,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是边
是边![]() 上一点,以点
上一点,以点![]() 为直角顶点,在
为直角顶点,在![]() 的右侧作等腰直角
的右侧作等腰直角![]() .
.
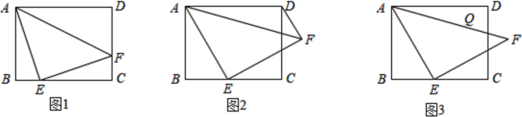
(1)如图1,当点![]() 在
在![]() 边上时,求
边上时,求![]() 的长;
的长;
(2)如图2,若![]() ,求
,求![]() 的长;
的长;
(3)如图3,若动点![]() 从点
从点![]() 出发,沿边
出发,沿边![]() 向右运动,运动到点
向右运动,运动到点![]() 停止,直接写出线段
停止,直接写出线段![]() 的中点
的中点![]() 的运动路径长.
的运动路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
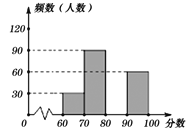
【题目】某市开展“弘扬中华传统文化”系列活动,为了解本次活动中竞赛项目“传统文化”笔试情况,随机抽查了部分参赛学生的成绩,整理并制作下列图表(尚未完整).请根据图表提供的信息,解答下列问题:
(1)本次调查的样本容量为_______;在表中:m=______,n=_______;
(2)补全频数分布直方图;
(3)若小聪同学的比赛成绩恰好是所有抽查学生成绩的中位数,则小聪同学的成绩落在_______________________分数段内;
(4)如果比赛成绩80分以上(含80分)为优秀,那么该竞赛项目的优秀率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算(直接写出结果)
(1)-4-3=
(2)13-(-3)=
(3)-8+(-2)=
(4)![]() ×(-1)=
×(-1)=
(5)-(-1![]() )2=
)2=
(6)![]() ÷(-2)=
÷(-2)=
(7)(-3)4×0=
(8)-1.2×![]() =
=
(9)|+7|-|-5|=
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李老师准备购买一套小户型商品房,他去售楼处了解情况得知.该户型商品房的单价是5000元/![]() ,面积如图所示(单位:m,卫生间的宽未定,设宽为xm),售房部为李老师提供了以下两种优惠方案:
,面积如图所示(单位:m,卫生间的宽未定,设宽为xm),售房部为李老师提供了以下两种优惠方案:
方案一:整套房的单价为5000元/![]() ,其中厨房可免费赠送一半的面积;
,其中厨房可免费赠送一半的面积;
方案二:整套房按原销售总金额的9.5折出售.

(1)用含x的代数式表示该户型商品房的面积及方案一、方案二中购买一套该户型商品房的总金额;
(2)当x=2时,通过计算说明哪种方案更优惠?优惠多少元?
(3)李老师因现金不够,于2019年10月在建行借了18万元住房贷款,贷款期限为10年,从开始贷款的下一个月起逐月偿还,贷款月利率是0.5%,每月应还的贷款本金数额为1500元(每月还款数额=每月应还的贷款本金数额+月利息,月利息=上月所剩贷款本金数额×月利率),假设贷款月利率不变,请求出李老师在借款后第n(![]() ,n是正整数)个月的还款数额.(用n的代数式表示)
,n是正整数)个月的还款数额.(用n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角△ABC中,∠C=90°,D为BC的中点,将△ABC折叠,使点A与点D重合,EF为折痕,则sin∠BED的值是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com