
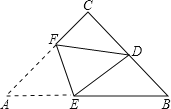
【题目】如图,在等腰直角△ABC中,∠C=90°,D为BC的中点,将△ABC折叠,使点A与点D重合,EF为折痕,则sin∠BED的值是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】分析:先根据翻折变换的性质得到△DEF≌△AEF,再根据等腰三角形的性质及三角形外角的性质可得到∠BED=CDF,设CD=1,CF=x,则CA=CB=2,再根据勾股定理即可求解.
详解:∵△DEF是△AEF翻折而成,
∴△DEF≌△AEF,∠A=∠EDF,
∵△ABC是等腰直角三角形,
∴∠EDF=45°,由三角形外角性质得∠CDF+45°=∠BED+45°,
∴∠BED=∠CDF,
设CD=1,CF=x,则CA=CB=2,
∴DF=FA=2-x,
∴在Rt△CDF中,由勾股定理得,
CF2+CD2=DF2,
即x2+1=(2-x)2,
解得:x=![]() ,
,
∴sin∠BED=sin∠CDF=![]() .
.
故选B.


科目:初中数学 来源: 题型:
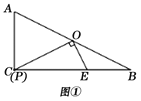
【题目】已知:在Rt△ABC中,∠ACB=90°,AC=4,BC=8,O是AB边的中点,P是AC边上的动点,OE⊥OP交BC边于点E,连接PE.
(1)如图①,当P与C重合时,线段PE的长为___________;
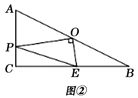
(2)如图②,当P在AC边上运动时,
①探究:线段PA,PE,EB之间的数量关系,并证明你的结论;
②若设PA=![]() ,PE2=y,求y与x之间的函数关系式及线段PE的最小值.
,PE2=y,求y与x之间的函数关系式及线段PE的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
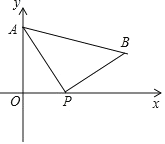
【题目】如图,A(0,4)是直角坐标系 y 轴上一点,动点 P 从原点 O 出发,沿 x 轴正半轴运动,速度为每秒 1 个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为 t 秒.
(1)若 AB∥x 轴,求 t 的值;
(2)若OP=![]() OA,求B点的坐标.
OA,求B点的坐标.
(3)当 t=3 时,x 轴上是否存在有一点 M,使得以 M、P、A 为顶点的三角形是等腰三角形,请直接写出点 M 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,点E,F分别在边AB,CD上,点G,H在对角线AC上,EF与AC相交于点O,AG=CH,BE=DF.
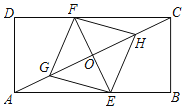
(1)求证:四边形EGFH是平行四边形;
(2)当EG=EH时,连接AF
①求证:AF=FC;
②若DC=8,AD=4,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,适宜采用全面调查(普查)方式的是( )
A.了解我国民众对乐天集团“萨德事件”的看法
B.调查我校某班学生喜欢上数学课的情况
C.了解湖南卫视《人们的名义》反腐剧的收视率
D.调查某类烟花爆竹燃放的安全情况
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某剧院的观众席的座位为扇形,且按下列分式设置:
排数(x) | 1 | 2 | 3 | 4 | … |
座位数(y) | 50 | 53 | 56 | 59 | … |
(1)按照上表所示的规律,当x每增加1时,y如何变化?
(2)写出座位数y与排数x之间的关系式;
(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知自行车与摩托车从甲地开往乙地,OA与BC分别表示它们与甲地距离s(千米)与时间t(小时)的关系,则:
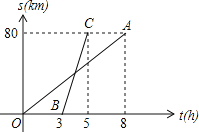
(1)摩托车每小时走 千米,自行车每小时走 千米;
(2)自行车出发后多少小时,它们相遇?
(3)摩托车出发后多少小时,他们相距10千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+(a+2)x+2(a≠0)与x轴交于点A(4,0),与y轴交于点B,在x轴上有一动点P(m,0)(0<m<4),过点P作x轴的垂线交直线AB于点N,交抛物线于点M.

(1)求a的值;
(2)若PN:MN=1:3,求m的值;
(3)如图2,在(2)的条件下,设动点P对应的位置是P1,将线段OP1绕点O逆时针旋转得到OP2,旋转角为α(0°<α<90°),连接AP2、BP2,求AP2+![]() BP2的最小值.
BP2的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com