
【题目】如图,已知自行车与摩托车从甲地开往乙地,OA与BC分别表示它们与甲地距离s(千米)与时间t(小时)的关系,则:
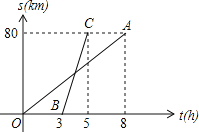
(1)摩托车每小时走 千米,自行车每小时走 千米;
(2)自行车出发后多少小时,它们相遇?
(3)摩托车出发后多少小时,他们相距10千米?
【答案】(1)40,10;(2)4小时;(3)摩托车出发后![]() 或
或![]() 或4小时,他们相距10千米
或4小时,他们相距10千米
【解析】
(1)根据图像可得BC为摩托车的图像可得时间和路程,就可以得到摩托车的速度;OA为自行车图像,由图像可得时间和路程,就可以得到自行车的速度;
(2)由图像可知自行车先出发3小时,由相遇时两车路程相等可列方程。
(3)由相遇前自行车在摩托车前,可用自行车路程-摩托车路程=10;
相遇后摩托车在自行车前,可用摩托车路程-自行车路程=10
最后摩托车达到终点不再行驶,则自行车距离终点10千米也为题中所求
(1)摩托车每小时走:80÷(5﹣3)=40(千米),
自行车每小时走:80÷8=10(千米).
故答案为:40,10;
(2)设自行车出发后x小时,它们相遇,
10x=40(x﹣3)
解得x=4.
(3)设摩托车出发后t小时,他们相距10千米;
①相遇前:10(t+3)﹣40t=10,
解得t=![]() ;
;
②相遇后:40t﹣10(t+3)=10,
解得:t=![]() ,
,
③摩托车到达终点10(t+3)=70,解得t=4
答:摩托车出发后![]() 或
或![]() 或4小时,他们相距10千米.
或4小时,他们相距10千米.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】计算(直接写出结果)
(1)-4-3=
(2)13-(-3)=
(3)-8+(-2)=
(4)![]() ×(-1)=
×(-1)=
(5)-(-1![]() )2=
)2=
(6)![]() ÷(-2)=
÷(-2)=
(7)(-3)4×0=
(8)-1.2×![]() =
=
(9)|+7|-|-5|=
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-2x-3,点P在该函数的图象上,点P到x轴、y轴的距离分别为d1、d2.设d=d1+d2,下列结论中: ①d没有最大值; ②d没有最小值; ③ -1<x<3时,d 随x的增大而增大; ④满足d=5的点P有四个.其中正确结论的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角△ABC中,∠C=90°,D为BC的中点,将△ABC折叠,使点A与点D重合,EF为折痕,则sin∠BED的值是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将平行四边形ABCD沿对角线BD进行折叠,折叠后点C落在点F处,DF交AB于点E.
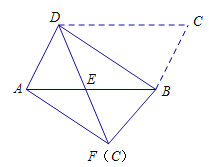
(1)求证:![]() ;
;
(2)判断AF与BD是否平行,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
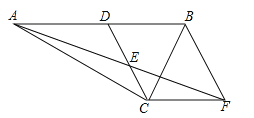
【题目】已知:如图,在Rt△ACB中,∠ACB=90°,点D是AB的中点,点E是CD的中点,过点C作CF∥AB叫AE的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若∠DCF=120°,DE=2,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,![]() 两点在数轴上,点
两点在数轴上,点![]() 对应的数为-15,
对应的数为-15,![]() ,
,![]() 两点分别从点
两点分别从点![]() 点
点![]() 同时出发,沿数轴正方向匀速运动,速度分别为每秒3个单位长度和每秒2个单位长度.
同时出发,沿数轴正方向匀速运动,速度分别为每秒3个单位长度和每秒2个单位长度.
(1)数轴上点![]() 对应的数是
对应的数是
(2)经过多少秒时,![]() 两点分别到原点的距离相等?
两点分别到原点的距离相等?
(3)当![]() 两点分别到点
两点分别到点![]() 的距离相等时,在数轴上点
的距离相等时,在数轴上点![]() 对应的数是
对应的数是
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() 与
与![]() 两个角的角平分线相交于点
两个角的角平分线相交于点![]() .
.
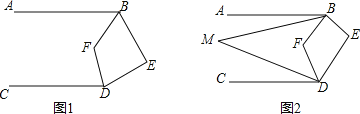
(1)如图1,若![]() ,求
,求![]() 的度数.
的度数.
(2)如图2,若![]() ,
,![]() ,试写出
,试写出![]() 与
与![]() 之间的数量关系并证明你的结论.
之间的数量关系并证明你的结论.
(3)若![]() ,
,![]() ,
,![]() ,请直接用含有
,请直接用含有![]() ,
,![]() 的代数式表示出
的代数式表示出![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在![]() 中,
中,![]() ,
,![]() 是
是![]() 边上的一个动点,将
边上的一个动点,将![]() 沿
沿![]() 所在直线折叠,使点
所在直线折叠,使点![]() 落在点
落在点![]() 处.
处.
(1)如图①,若点![]() 是
是![]() 的中点,连接
的中点,连接![]() .求证:四边形
.求证:四边形![]() 是平行四边形;
是平行四边形;
(2)如图②,若![]() ,求
,求![]() 的值.
的值.
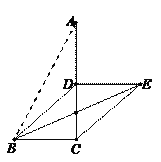
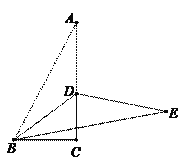
图① 图②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com