
【题目】已知![]() ,
,![]() 与
与![]() 两个角的角平分线相交于点
两个角的角平分线相交于点![]() .
.
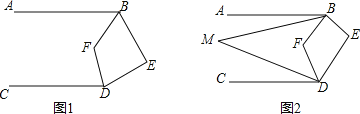
(1)如图1,若![]() ,求
,求![]() 的度数.
的度数.
(2)如图2,若![]() ,
,![]() ,试写出
,试写出![]() 与
与![]() 之间的数量关系并证明你的结论.
之间的数量关系并证明你的结论.
(3)若![]() ,
,![]() ,
,![]() ,请直接用含有
,请直接用含有![]() ,
,![]() 的代数式表示出
的代数式表示出![]() .
.
【答案】(1)140°;(2)∠BMD=![]() (360°-∠E),证明见解析; (3)∠BMD=
(360°-∠E),证明见解析; (3)∠BMD=![]()
【解析】
(1)过F点作FH∥AB,过E点作EG∥AB,根据平行线的传递性及平行线的性质可得∠ABE+∠CDE=360°-∠BED,根据平行线的性质可证∠BFD=∠ABF+∠CDF,再根据角平分线的定义求解即可;
(2)过M点作MN∥AB,同一可得∠BMD=∠ABM+∠CDM,由(1)可得∠ABF+∠CDF与∠BED的关系,再根据∠ABM =![]() ∠ABF,∠CDM=
∠ABF,∠CDM=![]() ∠CDF即可求解;
∠CDF即可求解;
(3)根据(2)中的过程进行推论,总结规律即可.
(1)过F点作FH∥AB,过E点作EG∥AB,如图:
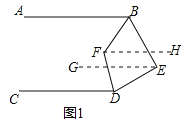
∵![]()
∴FH∥CD,EG∥CD
∴∠ABE+∠BEG=180°,∠GED+∠EDC=180°,∠ABF=∠BFH,∠HFD=∠FDC
∴∠ABE+∠BED+∠EDC=∠ABE+∠BEG+∠GED+∠EDC=360°,∠BFD=∠BFH+∠HFD=∠ABF+∠FDC
∴∠ABE+∠EDC =360°-∠BED
∵![]() 与
与![]() 两个角的角平分线相交于点
两个角的角平分线相交于点![]() .
.
∴∠ABF+∠FDC=![]() (∠ABE+∠EDC)=
(∠ABE+∠EDC)=![]() (360°-∠BED)
(360°-∠BED)
∵∠BED=80°
∴∠BFD=∠ABF+∠FDC=![]() =140°
=140°
(2)∠BMD=![]() (360°-∠E),证明:
(360°-∠E),证明:
过M点作MN∥AB,如图:
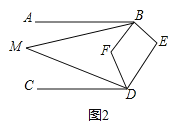
∵![]()
∴MN∥CD,
∴∠ABM=∠BMN,∠NMD=∠MDC
∴∠BMD=∠BMN+∠NMD=∠ABM+∠MDC
由(1)得:∠ABF+∠FDC=![]() (∠ABE+∠EDC)=
(∠ABE+∠EDC)=![]() (360°-∠E)
(360°-∠E)
∵∠ABM =![]() ∠ABF,∠CDM=
∠ABF,∠CDM=![]() ∠CDF
∠CDF
∴∠BMD=∠ABM+∠MDC=![]() (∠ABF+∠FDC)=
(∠ABF+∠FDC)=![]() (360°-∠E)
(360°-∠E)
(3)由(2)得:∠BMD=∠ABM+∠MDC,由(1)得:∠ABF+∠FDC=![]() (360°-∠BED)
(360°-∠BED)
∵![]() ,
,![]()
∴∠BMD=∠ABM+∠MDC=![]() (∠ABF+∠FDC)=
(∠ABF+∠FDC)=![]() (360°-∠BED)=
(360°-∠BED)=![]()


科目:初中数学 来源: 题型:
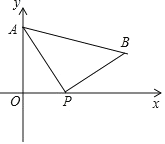
【题目】如图,A(0,4)是直角坐标系 y 轴上一点,动点 P 从原点 O 出发,沿 x 轴正半轴运动,速度为每秒 1 个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为 t 秒.
(1)若 AB∥x 轴,求 t 的值;
(2)若OP=![]() OA,求B点的坐标.
OA,求B点的坐标.
(3)当 t=3 时,x 轴上是否存在有一点 M,使得以 M、P、A 为顶点的三角形是等腰三角形,请直接写出点 M 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知自行车与摩托车从甲地开往乙地,OA与BC分别表示它们与甲地距离s(千米)与时间t(小时)的关系,则:
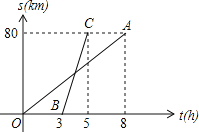
(1)摩托车每小时走 千米,自行车每小时走 千米;
(2)自行车出发后多少小时,它们相遇?
(3)摩托车出发后多少小时,他们相距10千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+(a+2)x+2(a≠0)与x轴交于点A(4,0),与y轴交于点B,在x轴上有一动点P(m,0)(0<m<4),过点P作x轴的垂线交直线AB于点N,交抛物线于点M.

(1)求a的值;
(2)若PN:MN=1:3,求m的值;
(3)如图2,在(2)的条件下,设动点P对应的位置是P1,将线段OP1绕点O逆时针旋转得到OP2,旋转角为α(0°<α<90°),连接AP2、BP2,求AP2+![]() BP2的最小值.
BP2的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
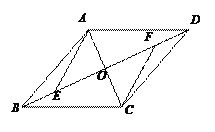
【题目】如图,在□ABCD中,AC、BD相交于点O,点E、F在BD上,且BE=DF.连
接AE、CF.
(1)求证△AOE≌△COF;
(2)若AC⊥EF,连接AF、CE,判断四边形AECF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一辆摩拜单车放在水平的地面上,车把头下方A处与坐垫下方B处在平行于地面的水平线上,A、B之间的距离约为49cm,现测得AC、BC与AB的夹角分别为45°与68°,若点C到地面的距离CD为28cm,坐垫中轴E处与点B的距离BE为4cm,求点E到地面的距离(结果保留一位小数).(参考数据:sin68°≈0.93,cos68°≈0.37,cot68°≈0.40)

查看答案和解析>>
科目:初中数学 来源: 题型:
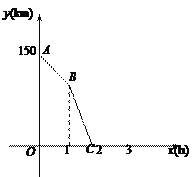
【题目】一辆货车从甲地出发以50 km/h的速度匀速驶往乙地,行驶1 h后,一辆轿车从乙地出发沿同一条路匀速驶往甲地.轿车行驶0.8 h后两车相遇.图中折线ABC表示两车之间的距离y(km)与货车行驶时间x(h)的函数关系.
(1)甲乙两地之间的距离是__________ km,轿车的速度是_________ km/h;
(2)求线段BC所表示的函数表达式;
(3)在图中画出货车与轿车相遇后的y(km)与x(h)的函数图像.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,将矩形![]() 折叠,使
折叠,使![]() 落在对角线
落在对角线![]() 上,折痕为
上,折痕为![]() ,点
,点![]() 落在点
落在点![]() 处,若
处,若![]() ,则
,则![]() ;
;
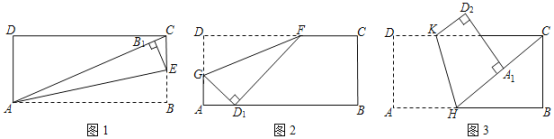
(2)小丽手中有一张矩形纸片,![]() ,
,![]() .她准备按如下两种方式进行折叠:
.她准备按如下两种方式进行折叠:
①如图2,点![]() 在这张矩形纸片的边
在这张矩形纸片的边![]() 上,将纸片折叠,使点
上,将纸片折叠,使点![]() 落在边
落在边![]() 上的点
上的点![]() 处,折痕为
处,折痕为![]() ,若
,若![]() ,求
,求![]() 的长;
的长;
②如图3,点![]() 在这张矩形纸片的边
在这张矩形纸片的边![]() 上,将纸片折叠,使
上,将纸片折叠,使![]() 落在射线
落在射线![]() 上,折痕为
上,折痕为![]() ,点
,点![]() ,
,![]() 分别落在
分别落在![]() ,
,![]() 处,若
处,若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com