
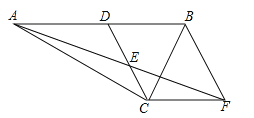
【题目】如图1,抛物线y=ax2+(a+2)x+2(a≠0)与x轴交于点A(4,0),与y轴交于点B,在x轴上有一动点P(m,0)(0<m<4),过点P作x轴的垂线交直线AB于点N,交抛物线于点M.

(1)求a的值;
(2)若PN:MN=1:3,求m的值;
(3)如图2,在(2)的条件下,设动点P对应的位置是P1,将线段OP1绕点O逆时针旋转得到OP2,旋转角为α(0°<α<90°),连接AP2、BP2,求AP2+![]() BP2的最小值.
BP2的最小值.
【答案】(1)![]() (2) 3 (3)
(2) 3 (3) ![]()
【解析】分析:(1)把A点坐标代入可得到关于a的方程,可求得a的值;
(2)由△OAB∽△PAN可用m表示出PN,且可表示出PM,由条件可得到关于m的方程,则可求得m的值;
(3)在y轴上取一点Q,使![]() ,可证得△P2OB∽△QOP2,则可求得Q点坐标,则可把AP2+
,可证得△P2OB∽△QOP2,则可求得Q点坐标,则可把AP2+![]() BP2化为AP2+QP2,利用三角形三边关系可知当A、P2、Q三点在一条线上时有最小值,则可求得答案.
BP2化为AP2+QP2,利用三角形三边关系可知当A、P2、Q三点在一条线上时有最小值,则可求得答案.
详解:(1)∵A(4,0)在抛物线上,
∴0=16a+4(a+2)+2,解得a=-![]() ;
;
(2)由(1)可知抛物线解析式为y=-![]() x2+
x2+![]() x+2,令x=0可得y=2,
x+2,令x=0可得y=2,
∴OB=2,
∵OP=m,
∴AP=4-m,
∵PM⊥x轴,
∴△OAB∽△PAN,
∴![]() ,即
,即![]() ,
,
∴PN=![]() (4-m),
(4-m),
∵M在抛物线上,
∴PM=-![]() m2+
m2+![]() m+2,
m+2,
∵PN:MN=1:3,
∴PN:PM=1:4,
∴-![]() m2+
m2+![]() m+2=4×
m+2=4×![]() (4-m),
(4-m),
解得m=3或m=4(舍去);
(3)在y轴上取一点Q,使![]() ,如图,
,如图,

由(2)可知P1(3,0),且OB=2,
∴![]() ,且∠P2OB=∠QOP2,
,且∠P2OB=∠QOP2,
∴△P2OB∽△QOP2,
∴![]() ,
,
∴当Q(0,![]() )时QP2=
)时QP2=![]() BP2,
BP2,
∴AP2+![]() BP2=AP2+QP2≥AQ,
BP2=AP2+QP2≥AQ,
∴当A、P2、Q三点在一条线上时,AP2+QP2有最小值,
∵A(4,0),Q(0,![]() ),
),
∴AQ=![]() ,即AP2+
,即AP2+![]() BP2的最小值为
BP2的最小值为![]() .
.


科目:初中数学 来源: 题型:
【题目】李老师准备购买一套小户型商品房,他去售楼处了解情况得知.该户型商品房的单价是5000元/![]() ,面积如图所示(单位:m,卫生间的宽未定,设宽为xm),售房部为李老师提供了以下两种优惠方案:
,面积如图所示(单位:m,卫生间的宽未定,设宽为xm),售房部为李老师提供了以下两种优惠方案:
方案一:整套房的单价为5000元/![]() ,其中厨房可免费赠送一半的面积;
,其中厨房可免费赠送一半的面积;
方案二:整套房按原销售总金额的9.5折出售.

(1)用含x的代数式表示该户型商品房的面积及方案一、方案二中购买一套该户型商品房的总金额;
(2)当x=2时,通过计算说明哪种方案更优惠?优惠多少元?
(3)李老师因现金不够,于2019年10月在建行借了18万元住房贷款,贷款期限为10年,从开始贷款的下一个月起逐月偿还,贷款月利率是0.5%,每月应还的贷款本金数额为1500元(每月还款数额=每月应还的贷款本金数额+月利息,月利息=上月所剩贷款本金数额×月利率),假设贷款月利率不变,请求出李老师在借款后第n(![]() ,n是正整数)个月的还款数额.(用n的代数式表示)
,n是正整数)个月的还款数额.(用n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角△ABC中,∠C=90°,D为BC的中点,将△ABC折叠,使点A与点D重合,EF为折痕,则sin∠BED的值是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
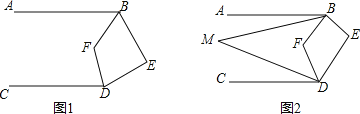
【题目】已知:如图,在Rt△ACB中,∠ACB=90°,点D是AB的中点,点E是CD的中点,过点C作CF∥AB叫AE的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若∠DCF=120°,DE=2,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,![]() 两点在数轴上,点
两点在数轴上,点![]() 对应的数为-15,
对应的数为-15,![]() ,
,![]() 两点分别从点
两点分别从点![]() 点
点![]() 同时出发,沿数轴正方向匀速运动,速度分别为每秒3个单位长度和每秒2个单位长度.
同时出发,沿数轴正方向匀速运动,速度分别为每秒3个单位长度和每秒2个单位长度.
(1)数轴上点![]() 对应的数是
对应的数是
(2)经过多少秒时,![]() 两点分别到原点的距离相等?
两点分别到原点的距离相等?
(3)当![]() 两点分别到点
两点分别到点![]() 的距离相等时,在数轴上点
的距离相等时,在数轴上点![]() 对应的数是
对应的数是
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】珠江流域某江段江水流向经过B、C、D三点拐弯后与原来相同,如图,若∠ABC=120°,∠BCD=80°,则∠CDE=__________度.

(第22题)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() 与
与![]() 两个角的角平分线相交于点
两个角的角平分线相交于点![]() .
.
(1)如图1,若![]() ,求
,求![]() 的度数.
的度数.
(2)如图2,若![]() ,
,![]() ,试写出
,试写出![]() 与
与![]() 之间的数量关系并证明你的结论.
之间的数量关系并证明你的结论.
(3)若![]() ,
,![]() ,
,![]() ,请直接用含有
,请直接用含有![]() ,
,![]() 的代数式表示出
的代数式表示出![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)若AD=5,BD=12,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节期间,某品牌粽子经销商销售甲、乙两种不同味道的粽子,已知一个甲种粽子和一个乙种粽子的进价之和为10元,每个甲种粽子的利润是4元,每个乙种粽子的售价比其进价的2倍少1元,小王同学买4个甲种粽子和3个乙种粽子一共用了61元.
(1)甲、乙两种粽子的进价分别是多少元?
(2)在(1)的前提下,经销商统计发现:平均每天可售出甲种粽子200个和乙种粽子150个.如果将两种粽子的售价各提高1元,则每天将少售出50个甲种粽子和40个乙种粽子.为使每天获取的利润更多,经销商决定把两种粽子的价格都提高x元.在不考虑其他因素的条件下,当x为多少元时,才能使该经销商每天销售甲、乙两种粽子获取的利润为1190元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com