
【题目】端午节期间,某品牌粽子经销商销售甲、乙两种不同味道的粽子,已知一个甲种粽子和一个乙种粽子的进价之和为10元,每个甲种粽子的利润是4元,每个乙种粽子的售价比其进价的2倍少1元,小王同学买4个甲种粽子和3个乙种粽子一共用了61元.
(1)甲、乙两种粽子的进价分别是多少元?
(2)在(1)的前提下,经销商统计发现:平均每天可售出甲种粽子200个和乙种粽子150个.如果将两种粽子的售价各提高1元,则每天将少售出50个甲种粽子和40个乙种粽子.为使每天获取的利润更多,经销商决定把两种粽子的价格都提高x元.在不考虑其他因素的条件下,当x为多少元时,才能使该经销商每天销售甲、乙两种粽子获取的利润为1190元?
【答案】(1)甲种粽子的进价是6元/个,乙种粽子的进价是4元/个.(2)1元.
【解析】
试题分析:(1)设甲种粽子的进价是x元/个,乙种粽子的进价是y元/个,根据等量关系:一个甲种粽子和一个乙种粽子的进价之和为10元,小王同学买4个甲种粽子和3个乙种粽子一共用了61元,列出方程组即可求解;
(2)根据每天销售甲、乙两种粽子获取的利润为1190元,列出方程即可求解.
试题解析:(1)设甲种粽子的进价是x元/个,乙种粽子的进价是y元/个,则
![]() ,
,
解得![]() .
.
故甲种粽子的进价是6元/个,乙种粽子的进价是4元/个.
(2)依题意有(4+x)+(3+x)(150-40x)=1190,
3x2-x-2=0,
解得x1=1,x2=-![]() ,
,
∵x>0,
∴x=1.
答:当x为1元时,才能使该经销商每天销售甲、乙两种粽子获取的利润为1190元.


科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+(a+2)x+2(a≠0)与x轴交于点A(4,0),与y轴交于点B,在x轴上有一动点P(m,0)(0<m<4),过点P作x轴的垂线交直线AB于点N,交抛物线于点M.

(1)求a的值;
(2)若PN:MN=1:3,求m的值;
(3)如图2,在(2)的条件下,设动点P对应的位置是P1,将线段OP1绕点O逆时针旋转得到OP2,旋转角为α(0°<α<90°),连接AP2、BP2,求AP2+![]() BP2的最小值.
BP2的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做等对角四边形.请解决下列问题:
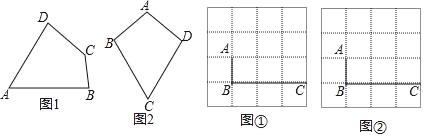
(1)已知:如图1,四边形ABCD是等对角四边形,∠A≠∠C,∠A=70°,∠B=75°,则∠C= °,∠D= °
(2)在探究等对角四边形性质时:
小红画了一个如图2所示的等对角四边形ABCD,其中,∠ABC=∠ADC,AB=AD,此时她发现CB=CD成立,请你证明该结论;
(3)图①、图②均为4×4的正方形网格,线段AB、BC的端点均在网点上.按要求在图①、图②中以AB和BC为边各画一个等对角四边形ABCD.
要求:四边形ABCD的顶点D在格点上,所画的两个四边形不全等.
(4)已知:在等对角四边形ABCD中,∠DAB=60°,∠ABC=90°,AB=5,AD=4,求对角线AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=9,AB=12,BC=15,P为BC边上一动点,PG⊥AC于点G,PH⊥AB于点H.
(1)求证:四边形AGPH是矩形;
(2)在点P的运动过程中,GH的长度是否存在最小值?若存在,请求出最小值,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举行“传承好家风”征文比赛,已知每篇参赛征文成绩记m分(60≤m≤100),组委会从1000篇征文中随机抽取了部分参赛征文,统计了他们的成绩,并绘制了如下不完整的两幅统计图表.


请根据以上信息,解决下列问题:
(1)征文比赛成绩频数分布表中c的值是________;
(2)补全征文比赛成绩频数分布直方图;
(3)若80分以上(含80分)的征文将被评为一等奖,试估计全市获得一等奖征文的篇数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,将矩形![]() 折叠,使
折叠,使![]() 落在对角线
落在对角线![]() 上,折痕为
上,折痕为![]() ,点
,点![]() 落在点
落在点![]() 处,若
处,若![]() ,则
,则![]() ;
;
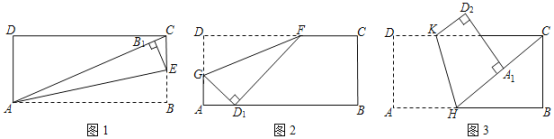
(2)小丽手中有一张矩形纸片,![]() ,
,![]() .她准备按如下两种方式进行折叠:
.她准备按如下两种方式进行折叠:
①如图2,点![]() 在这张矩形纸片的边
在这张矩形纸片的边![]() 上,将纸片折叠,使点
上,将纸片折叠,使点![]() 落在边
落在边![]() 上的点
上的点![]() 处,折痕为
处,折痕为![]() ,若
,若![]() ,求
,求![]() 的长;
的长;
②如图3,点![]() 在这张矩形纸片的边
在这张矩形纸片的边![]() 上,将纸片折叠,使
上,将纸片折叠,使![]() 落在射线
落在射线![]() 上,折痕为
上,折痕为![]() ,点
,点![]() ,
,![]() 分别落在
分别落在![]() ,
,![]() 处,若
处,若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙二人同时从学校出发,沿同一方向匀速行走,![]() 后,甲加快速度继续匀速行走(加速的时间忽略不计),乙始终匀速行走,两人都走了
后,甲加快速度继续匀速行走(加速的时间忽略不计),乙始终匀速行走,两人都走了![]() .两人在行走过程中得到如下表所示的信息:
.两人在行走过程中得到如下表所示的信息:
离开学校的时间 |
|
|
|
|
甲离学校的距离 |
|
|
|
|
乙离学校的距离 |
|
|
|
|
(1)根据题意,甲出发时的速度为_______![]() ,乙的速度为______
,乙的速度为______![]() ;
;
(2)求表中![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:顶点、开口大小相同,开口方向相反的两个二次函数互为“反簇二次函数”.
(1)已知二次函数y=﹣(x﹣2)2+3,则它的“反簇二次函数”是__________________;
(2)已知关于x的二次函数y1=2x2﹣2mx+m+1和y2=ax2+bx+c,其中y1的图像经过点(1,1).若y1+y2与y1互为“反簇二次函数”.求函数y2的表达式,并直接写出当0≤x≤3时,y2的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com