
����Ŀ�����壺���㡢���ڴ�С��ͬ�����ڷ����෴���������κ�����Ϊ�����ض��κ�������
��1����֪���κ���y=��(x��2)2��3�������ġ����ض��κ�������__________________��
��2����֪����x�Ķ��κ���y1=2x2��2mx��m+1��y2=ax2+bx��c������y1��ͼ���㣨1��1��.��y1��y2��y1��Ϊ�����ض��κ�����.����y2�ı���ʽ����ֱ��д����0��x��3ʱ��y2����Сֵ��
���𰸡�(1)��y=��x��2��2+3��(2)����16��
��������������(1)�����ݡ����ض��κ������Ķ���ó��𰸣�(2)������y1��ͼ����A��1,1�����m��ֵ��Ȼ��ó�y1+y2�ĺ�������ʽ�����ݡ����ض��κ������Ķ���ó�a��b��c��ֵ���Ӷ��ó�y2�ĺ�������ʽ�����ݶ��κ��������ʵó���Сֵ��
��⣺��1��y=��x��2��2+3
��2����y1��ͼ����A��1,1���� ��2��2m+m+2=2�� ���m=2��
��y1=2x2��4x+3=2��x��1��2+1�� ��y1+y2=2x2��4x+3+ax2+bx+c=��a+2��x2+��b��4��x+c+3��
��y1+y2��y1Ϊ�����ض��κ������� ��y1+y2=-2��x��1��2+1=��2x2+4x��1��
��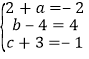 �����
�����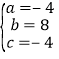 �� �ຯ��y2�ı���ʽΪ��y2=��4x2+8x��4��
�� �ຯ��y2�ı���ʽΪ��y2=��4x2+8x��4��
��0��x��3ʱ��y2����СֵΪ��16��


 100�ִ�����ĩ���ϵ�д�
100�ִ�����ĩ���ϵ�д� ��У���˿��ֿ���ϵ�д�
��У���˿��ֿ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ڼ䣬ijƷ�����Ӿ��������ۼס������ֲ�ͬζ�������ӣ���֪һ���������Ӻ�һ���������ӵĽ���֮��Ϊ10Ԫ��ÿ���������ӵ�������4Ԫ��ÿ���������ӵ��ۼ۱�����۵�2����1Ԫ��С��ͬѧ��4���������Ӻ�3����������һ������61Ԫ��
��1���ס����������ӵĽ��۷ֱ��Ƕ���Ԫ��
��2������1����ǰ���£�������ͳ�Ʒ��֣�ƽ��ÿ����۳���������200������������150����������������ӵ��ۼ۸����1Ԫ����ÿ�콫���۳�50���������Ӻ�40������������Ϊʹÿ���ȡ��������࣬�����̾������������ӵļ۸����xԪ���ڲ������������ص������£���xΪ����Ԫʱ������ʹ�þ�����ÿ�����ۼס����������ӻ�ȡ������Ϊ1190Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ڡ����ҹ��Ĵ�ͳ�ѽڣ���������гԡ����ӡ���ϰ�ף� ����ijʳƷ��Ϊ�˽������ȥ�������Ϻõ������ա���ɳ���ա��������ա���������(���·ֱ���A��B��C��D��ʾ)�����ֲ�ͬ��ζ���ӵ�ϲ��������ڽ�ǰ��ij��������������˳������飬��������������Ƴ���������ͳ��ͼ(�в�����)�� �����������Ϣ�ش�
(1)���βμӳ�������ľ����ж����ˣ�
(2)��������������ͼ����������
(3)����������8000�ˣ�����ư���D�յ�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼֱ������ϵ�ڣ��ı���AOBC�DZ߳�Ϊ2�����Σ�EΪ��OB���е㣬����AE��Խ���OC���ڵ�D���ҡ�BCO=��EAO�����D����Ϊ�� ��
A. ��![]() ��
��![]() �� B. ��1��
�� B. ��1��![]() �� C. ��
�� C. ��![]() ��
��![]() �� D. ��1��
�� D. ��1��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�δ��ͻ����ί���������˻����Ļ���̣��ڲٿ����˻�ʱӦ�����ֳ�״�����ڸ߶ȣ���֪���˻����������½��������ٶ���ͬ�������˻��ķ��и߶�Ϊy���ף����ٿ����˻���ʱ��Ϊx���֣���y��x֮��ĺ���ͼ����ͼ��ʾ.
��1�����˻����ٶ�Ϊ________��/�֣�
��2�����߶�BC����ʾ��y��x֮�亯������ʽ��
��3�����˻���50���Ͽճ�������ʱ��Ϊ_________�֣���ֱ��������
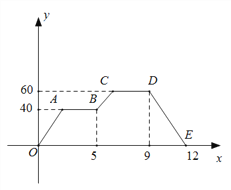
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�д�![]() ��
��![]() ��
��![]() �տ�ʼʵʩ���ݵ���ƣ����������õ�۸����£�
�տ�ʼʵʩ���ݵ���ƣ����������õ�۸����£�
���� | ���õ��� | ��� ����λ��Ԫ | |
���^�� | ���ļ��� | ||
�� | ������ | ������ |
|
�� | ���� | ���� |
|
�� | ���� | ���� |
|
������ij�û�![]() ��
��![]() �µ��õ���Ϊ
�µ��õ���Ϊ![]() �ȣ����轻���Ϊ��
�ȣ����轻���Ϊ��
![]() ��Ԫ����
��Ԫ����
��1��������![]() ��
��![]() �µ��õ���Ϊ
�µ��õ���Ϊ![]() �ȣ����轻��Ѷ���Ԫ��
�ȣ����轻��Ѷ���Ԫ��
��2��������![]() ��
��![]() �º�
�º�![]() ���õ�����ͬ���������
���õ�����ͬ���������![]() Ԫ����С����
Ԫ����С����![]() �·��ö��ٶȵ磿
�·��ö��ٶȵ磿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������й���ѧʷ�ϵ���Ҫ��������������֪�ĺ�����������������Ҫ���ϣ�����������Ŵ��㷨��������֤��������������������ı������Ƕ�������ѧ��չˮƽ����ʶ�����м������и����ˣ�����һ��֯��ʮ�ߣ����߶���֯��ʮ�ߣ���������֯��ʮ�ߣ������й���ʮ�ߣ��ʸ��ܼ��Σ������ģ�����λŮ����֯��������1��֯��50�ߣ�����2��֯��50�ߣ���3��֯��50�ߣ��������������ͬ���50��֯����������ÿ��֯�����ߣ���������һ������x�����֯����������з���Ϊ________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ǹ������¶��壺˳����������һ���ı��θ����е����õ��ı��ν��е��ı��Σ�

��1����ͼ1���ı���ABCD�У���E��F��G��H�ֱ�Ϊ��AB��BC��CD��DA���е㣮��֤���е��ı���EFGH��ƽ���ı��Σ�
��2����ͼ2����P���ı���ABCD��һ�㣬������PA=PB��PC=PD����APB=��CPD����E��F��G��H�ֱ�Ϊ��AB��BC��CD��DA���е㣬�����е��ı���EFGH����״����֤����IJ��룻
��3�����ı䣨2���е�������ʹ��APB=��CPD=90�㣬�����������䣬ֱ��д���е��ı���EFGH����״��������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������һ�ַdz���Ҫ����ѧ���������һ�����ṩ����֪�����а���������������ǿ��Է������������⣮���磺��|x|=2��|y|=3��x+y��ֵ��
�������x=2��y=3ʱ��x+y=5
�������x=2��y=��3ʱ��x+y=��1
�������x=��2��y=3ʱ��x+y=1
�������x=��2��y=��3ʱ��x+y=��5
���ԣ�x+y��ֵΪ1����1��5����5��
���ε�ѧϰ������Ҳ�����Ƶ������
���⣨1������֪��A��B��C��һ��ֱ���ϣ���AB=8��BC=3����AC��Ϊ���٣�
ͨ���������Ƿ��֣�������������������
���������C�ڵ�B���Ҳ�ʱ����ͼ1����ʱ��AC=�� ��
���������C�ڵ�B�����ʱ����ͼ2����ʱ��AC=�� ��
ͨ���������⣬���Ƿ��֣�������ͼ���������Ǹ��õĽ��з��࣮
���⣨2������ͼ3�������ϵ�A�͵�B��ʾ�����ֱ��ǩ�1��2����C��������һ�㣬��BC=2AB�����C��ʾ�����Ƕ��٣�
��������1������ͼ�Σ����ͼ��д��������ͽ����
���⣨3������O��ֱ��AB��һ�㣬��OΪ�˵�������OC��OD��ʹ��AOC=60�㣬OCOD������BOD�Ķ���������ͼ�Σ�ֱ��д�������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com