
����Ŀ��ij�д�![]() ��
��![]() ��
��![]() �տ�ʼʵʩ���ݵ���ƣ����������õ�۸����£�
�տ�ʼʵʩ���ݵ���ƣ����������õ�۸����£�
���� | ���õ��� | ��� ����λ��Ԫ | |
���^�� | ���ļ��� | ||
�� | ������ | ������ |
|
�� | ���� | ���� |
|
�� | ���� | ���� |
|
������ij�û�![]() ��
��![]() �µ��õ���Ϊ
�µ��õ���Ϊ![]() �ȣ����轻���Ϊ��
�ȣ����轻���Ϊ��
![]() ��Ԫ����
��Ԫ����
��1��������![]() ��
��![]() �µ��õ���Ϊ
�µ��õ���Ϊ![]() �ȣ����轻��Ѷ���Ԫ��
�ȣ����轻��Ѷ���Ԫ��
��2��������![]() ��
��![]() �º�
�º�![]() ���õ�����ͬ���������
���õ�����ͬ���������![]() Ԫ����С����
Ԫ����С����![]() �·��ö��ٶȵ磿
�·��ö��ٶȵ磿
���𰸡���1��222.5Ԫ����5��550��
��������
��1������С�����õ�400�ȴ��ڵ�3�������Ե�ѷ���������ӵõ����ֱ���ݱ�����㼴�ɵó��𰸣�
��2��ͨ�����㷢��С����8�·��õ糬��450�ȣ�Ȼ����8�·��õ�x�ȣ����������г����̣�Ȼ��ⷽ�̼��ɵó��𰸣�
��1������![]() ��
��![]() �µ��õ���Ϊ
�µ��õ���Ϊ![]() �ȣ����轻���
�ȣ����轻���
![]() ��Ԫ����
��Ԫ����
��2����8��9�·�ÿ�����õ�450�ȣ�
8�·�Ӧ����ѣ�![]() ��Ԫ��
��Ԫ��
9�·�Ӧ����ѣ�![]() ��Ԫ��
��Ԫ��
��8��9�¹�����ѣ�![]()
����8��9�·�ÿ�����õ糬��450��
��8��9�·�ÿ�����õ�x�ȣ�
8�·�Ӧ����ѣ�![]() ��Ԫ��
��Ԫ��
9�·�Ӧ����ѣ�![]() ��Ԫ��
��Ԫ��
��8��9�¹�����ѣ�![]() ��Ԫ��
��Ԫ��
����������
![]()
���![]()
��С����![]() �·���550�ȵ�
�·���550�ȵ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�о��������кüҷ������ı�������֪ÿƪ�������ijɼ���m�֣�60��m��100������ί���1000ƪ�����������ȡ�˲��ֲ������ģ�ͳ�������ǵijɼ��������������²�����������ͳ��ͼ��.


�����������Ϣ������������⣺
��1�����ı����ɼ�Ƶ���ֲ�����c��ֵ��________��
��2����ȫ���ı����ɼ�Ƶ���ֲ�ֱ��ͼ��
��3����80�����ϣ���80�֣������Ľ�����Ϊһ�Ƚ����Թ���ȫ�л��һ�Ƚ����ĵ�ƪ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
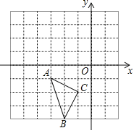
����Ŀ����ͼ����ֱ������ϵ�У�ÿ��С�����DZ߳�Ϊ![]() �������Σ�
�������Σ�![]() �Ķ�����ڸ���ϣ���
�Ķ�����ڸ���ϣ���![]() ��������
��������![]() ��
��
![]() �Ƚ�
�Ƚ�![]() ��
��![]() ������������ƽ��
������������ƽ��![]() ����λ���ȣ�����
����λ���ȣ�����![]() �Ḻ��������ƽ��
�Ḻ��������ƽ��![]() ����λ���ȵõ�
����λ���ȵõ�![]() ������
������![]() ����
����![]() ������________��
������________��
![]() ��
��![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() ���õ�
���õ�![]() ������
������![]() ���������
���������![]() ��������________��
��������________��
![]() ���Ƿ��ֵ�
���Ƿ��ֵ�![]() ��
��![]() ����ij�����ĶԳƣ��Գ����ĵ�������________��
����ij�����ĶԳƣ��Գ����ĵ�������________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У���E�DZ�CD���е㣬����BE���ӳ�����AD�ӳ����ڵ�F������BD��CF.
��1����֤����CEB�ա�DEF��
��2����AB=BF�����ж��ı���BCFD����״����֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺���㡢���ڴ�С��ͬ�����ڷ����෴���������κ�����Ϊ�����ض��κ�������
��1����֪���κ���y=��(x��2)2��3�������ġ����ض��κ�������__________________��
��2����֪����x�Ķ��κ���y1=2x2��2mx��m+1��y2=ax2+bx��c������y1��ͼ���㣨1��1��.��y1��y2��y1��Ϊ�����ض��κ�����.����y2�ı���ʽ����ֱ��д����0��x��3ʱ��y2����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���û����ֱ�ƴ��һ����������ɵ�ͼ�κ�һ����������ɵ�ͼ�Σ����������κ�������һ������2020������������εĸ����������εĸ�����4�����������εĸ����ǣ� ��

A.402 B.406 C.410 D.420
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѧ���ϣ���ʦ���һ����������ֱ�ߺ�Բ������ABΪ�ĵ���ֱ��������ABC����
С�����������£�
�ٷֱ��Ե�A��BΪԲ�ģ�����![]() AB���������ڵ�M��N��
AB���������ڵ�M��N��
����ֱ��MN����AB�ڵ�O��
���Ե�OΪԲ�ģ�OAΪ�뾶������Բ����ֱ��MN�ڵ�C��
������AC��BC��
���ԣ���ABC��Ϊ�������ĵ���ֱ����������
�����С������������ֱ�ߺ�Բ������ABΪ�ĵ���ֱ��������ABC����������ͼ�ۼ������������������� ��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���±����������ƶ��绰�Ʒѷ�ʽ��

˵������ʹ�÷ѹ̶���ȡ�����в�����ʱ�䲻���շѣ����г�ʱ���ּ��ճ�ʱ�ѣ�������ѣ�
��1��������ij������ͨ��ʱ��Ϊ700���ӣ���������ʽһ�Ʒ��� Ԫ������ʽ���Ʒ��� Ԫ���ú�![]() �Ĵ���ʽ��ʾ������������ʽһ�Ʒ���60Ԫ��������ͨ��ʱ��Ϊ ���ӣ�
�Ĵ���ʽ��ʾ������������ʽһ�Ʒ���60Ԫ��������ͨ��ʱ��Ϊ ���ӣ�
��2������ʽ�������г�ʱ��![]() ��Ԫ/���ӣ����Ƿ����ij����ͨ��ʱ��
��Ԫ/���ӣ����Ƿ����ij����ͨ��ʱ��![]() �����ӣ�������ʽһ�ͷ�ʽ���ļƷ���ȣ������ڣ������
�����ӣ�������ʽһ�ͷ�ʽ���ļƷ���ȣ������ڣ������![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
��3��������ʱ��Ϊ750����ʱ�����ַ�ʽ�ļƷ���ȣ�ֱ��д��![]() ��ֵΪ ������ͨ�����������ֱ�Ӹ�����������ͨ��ʱ��
��ֵΪ ������ͨ�����������ֱ�Ӹ�����������ͨ��ʱ��![]() �����ӣ�����ʲô����ʱ��ѡ��ʽ��ʡǮ��
�����ӣ�����ʲô����ʱ��ѡ��ʽ��ʡǮ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ACB���ECD���ǵ���ֱ�������Σ���ACB����ECD��90����DΪAB���ϵ�һ�㣬

��1����˵������EAC����B ��
��2����AD��15��BD��36����DE�ij���
��3������D��A��B֮���ƶ�������DΪ ʱ��AC��DE����ƽ��.
��ֱ��д���𰸣�����˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com