练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

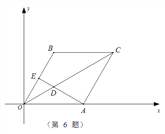
    【题目】在如图直角坐标系内，四边形AOBC是边长为2的菱形，E为边OB的中点，连结AE与对角线OC交于点D，且∠BCO=∠EAO，则点D坐标为（ ）

    A. （，） B. （1，） C. （，） D. （1，）

    【答案】D

    【解析】分析：首先根据菱形的性质得出△AOD为等腰三角形，根据菱形的性质得出∠BOA=2∠AOE，结合AO=2OE得出△AOD为底角为30°角的等腰三角形，从而得出点D的坐标．

    详解：∵BC∥OA， ∴∠BCO=∠COA， 又∵∠BCO=∠EAO， ∴∠COA=∠EAO，

    ∴△AOD为等腰三角形， ∴点D的横坐标为1， ∵四边形OACB为菱形，

    ∴∠BOA=2∠AOE， ∵AO=2OE， ∴∠DAO=∠DOA=30°，

    ∴点D的纵坐标为， ∴点D的坐标为(1，)．故选D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】我们定义：有一组对角相等而另一组对角不相等的凸四边形叫做等对角四边形．请解决下列问题：

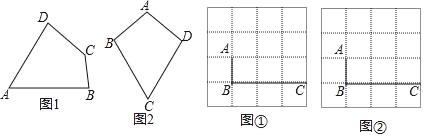
    （1）已知：如图1，四边形ABCD是等对角四边形，∠A≠∠C，∠A=70°，∠B=75°，则∠C=　 　°，∠D=　 　°

    （2）在探究等对角四边形性质时：

    小红画了一个如图2所示的等对角四边形ABCD，其中，∠ABC=∠ADC，AB=AD，此时她发现CB=CD成立，请你证明该结论；

    （3）图①、图②均为4×4的正方形网格，线段AB、BC的端点均在网点上．按要求在图①、图②中以AB和BC为边各画一个等对角四边形ABCD．

    要求：四边形ABCD的顶点D在格点上，所画的两个四边形不全等．

    （4）已知：在等对角四边形ABCD中，∠DAB=60°，∠ABC=90°，AB=5，AD=4，求对角线AC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙二人同时从学校出发，沿同一方向匀速行走，后，甲加快速度继续匀速行走(加速的时间忽略不计)，乙始终匀速行走，两人都走了.两人在行走过程中得到如下表所示的信息：

    离开学校的时间

    甲离学校的距离

    乙离学校的距离

    （1）根据题意，甲出发时的速度为_______，乙的速度为______；

    （2）求表中的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

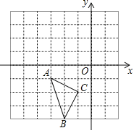
    【题目】如图，在直角坐标系中，每个小方格都是边长为的正方形，的顶点均在格点上，点的坐标是．

    先将沿轴正方向向上平移个单位长度，再沿轴负方向向左平移个单位长度得到，画出，点坐标是________；

    将绕点逆时针旋转，得到，画出，并求出点的坐标是________；

    我们发现点、关于某点中心对称，对称中心的坐标是________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一次禁毒宣传活动中，某执勤小组乘车沿东西向公路进行安全维护，如果约定向东为正，向西为负，行驶记录如下（单位：米）：+18，-9，+7，-14，-3，+13，-8，-6，+15，+6．

    （1）执勤过程中，最远处离出发点有多远？

    （2）若汽车行驶每千米耗油量为升，求这次执勤的汽车共耗油多少升？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在□ABCD中，点E是边CD的中点，连接BE并延长，交AD延长线于点F，连接BD、CF.

    （1）求证：△CEB≌△DEF；

    （2）若AB=BF，试判断四边形BCFD的形状，并证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：顶点、开口大小相同，开口方向相反的两个二次函数互为“反簇二次函数”．

    （1）已知二次函数y=﹣(x﹣2)2＋3，则它的“反簇二次函数”是__________________；

    （2）已知关于x的二次函数y1=2x2﹣2mx＋m+1和y2=ax2+bx＋c，其中y1的图像经过点（1，1）.若y1＋y2与y1互为“反簇二次函数”.求函数y2的表达式，并直接写出当0≤x≤3时，y2的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在数学课上，老师提出一个问题“用直尺和圆规作以AB为底的等腰直角三角形ABC”．

    小美的作法如下：

    ①分别以点A，B为圆心，大于AB作弧，交于点M，N；

    ②作直线MN，交AB于点O；

    ③以点O为圆心，OA为半径，作半圆，交直线MN于点C；

    ④连结AC，BC．

    所以，△ABC即为所求作的等腰直角三角形．

    请根据小美的作法，用直尺和圆规作以AB为底的等腰直角三角形ABC，并保留作图痕迹．这种作法的依据是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

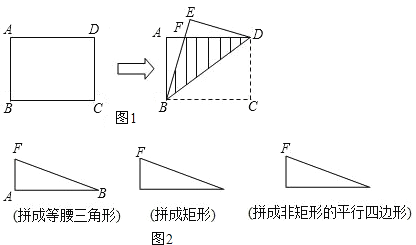
    【题目】已知：如图1，把一张矩形纸片ABCD沿对角线BD折叠，将重合部分（△BFD）剪去，得到△ABF和△EDF．

    （1）求证：FB=FD；

    （2）求证：△ABF≌△EDF；

    （3）将△ABF与△EDF不重合地拼在一起，可拼成特殊三角形和特殊四边形，请你按照下列要求将拼图补画完整（图2）．

    查看答案和解析>>

    同步练习册答案