
【题目】我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做等对角四边形.请解决下列问题:
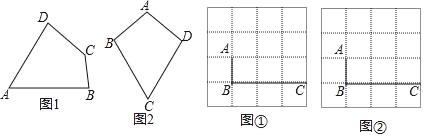
(1)已知:如图1,四边形ABCD是等对角四边形,∠A≠∠C,∠A=70°,∠B=75°,则∠C= °,∠D= °
(2)在探究等对角四边形性质时:
小红画了一个如图2所示的等对角四边形ABCD,其中,∠ABC=∠ADC,AB=AD,此时她发现CB=CD成立,请你证明该结论;
(3)图①、图②均为4×4的正方形网格,线段AB、BC的端点均在网点上.按要求在图①、图②中以AB和BC为边各画一个等对角四边形ABCD.
要求:四边形ABCD的顶点D在格点上,所画的两个四边形不全等.
(4)已知:在等对角四边形ABCD中,∠DAB=60°,∠ABC=90°,AB=5,AD=4,求对角线AC的长.
【答案】(1)140°,75°;(2)证明见解析;(3)见解析;(4)2![]() 或2
或2![]() .
.
【解析】
试题(1)根据四边形ABCD是“等对角四边形”得出∠D=∠B=75°,根据多边形内角和定理求出∠C即可;
(2)连接BD,根据等边对等角得出∠ABD=∠ADB,求出∠CBD=∠CDB,根据等腰三角形的判定得出即可;
(3)根据等对角四边形的定义画出图形即可求解;
(4)分两种情况:①当∠ADC=∠ABC=90°时,延长AD,BC相交于点E,先用含30°角的直角三角形的性质求出AE,得出DE,再用三角函数求出CD,由勾股定理求出AC;
②当∠BCD=∠DAB=60°时,过点D作DM⊥AB于点M,DN⊥BC于点N,则∠AMD=90°,四边形BNDM是矩形,先求出AM、DM,再由矩形的性质得出DN=BM=3,BN=DM=2![]() ,求出CN、BC,根据勾股定理求出AC即可.
,求出CN、BC,根据勾股定理求出AC即可.
试题解析:
(1)解:∵四边形ABCD是“等对角四边形”,∠A≠∠C,∠A=70°,∠B=75°,
∴∠D=∠B=75°,
∴∠C=360°﹣75°﹣75°﹣70°=140°;
(2)证明:如图2,连接BD,
∵AB=AD,
∴∠ABD=∠ADB,
∵∠ABC=∠ADC,
∴∠ABC﹣∠ABD=∠ADC﹣∠ADB,
∴∠CBD=∠CDB,
∴CB=CD;
(3)如图所示:
(4)解:分两种情况:
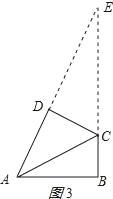
①当∠ADC=∠ABC=90°时,延长AD,BC相交于点E,如图3所示:
∵∠ABC=90°,∠DAB=60°,AB=5,
∴∠E=30°,
∴AE=2AB=10,
∴DE=AE﹣AD=10﹣4═6,
∵∠EDC=90°,∠E=30°,
∴CD=2![]() ,
,
∴AC=![]() ;
;
②当∠BCD=∠DAB=60°时,
过点D作DM⊥AB于点M,DN⊥BC于点N,如图4所示:
则∠AMD=90°,四边形BNDM是矩形,
∵∠DAB=60°,
∴∠ADM=30°,
∴AM=![]() AD=2,
AD=2,
∴DM=2![]() ,
,
∴BM=AB﹣AM=5﹣2=3,
∵四边形BNDM是矩形,
∴DN=BM=3,BN=DM=2![]() ,
,
∵∠BCD=60°,
∴CN=![]() ,
,
∴BC=CN+BN=3![]() ,
,
∴AC=![]() .
.
综上所述:AC的长为![]() 或
或![]() .
.
故答案为:140,75.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ACB中,∠ACB=90°,点D是AB的中点,点E是CD的中点,过点C作CF∥AB叫AE的延长线于点F.
(1)求证:△ADE≌△FCE;
(2)若∠DCF=120°,DE=2,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)若AD=5,BD=12,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在![]() 中,
中,![]() ,
,![]() 是
是![]() 边上的一个动点,将
边上的一个动点,将![]() 沿
沿![]() 所在直线折叠,使点
所在直线折叠,使点![]() 落在点
落在点![]() 处.
处.
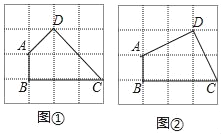
(1)如图①,若点![]() 是
是![]() 的中点,连接
的中点,连接![]() .求证:四边形
.求证:四边形![]() 是平行四边形;
是平行四边形;
(2)如图②,若![]() ,求
,求![]() 的值.
的值.
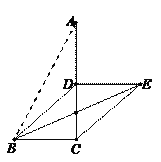
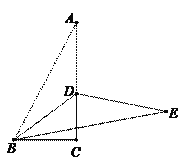
图① 图②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市在各校推广大阅读活动,初二(1)班为了解2月份全班学生课外阅读的情况,调查了全班学生2月份读书的册数,并根据调查结果绘制了如下不完整的条形统计图和扇形统计图:
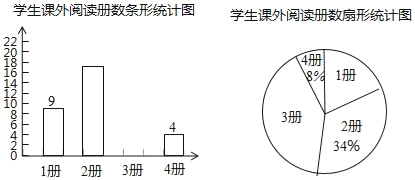
根据以上信息解决下列问题:
(1)参加本次问卷调查的学生共有 人,其中2月份读书2册的学生有 人;
(2)补全条形统计图,并求扇形统计图中读书3册所对应扇形的圆心角度数;
(3)在读书4册的学生中恰好有2名男生和2名女生,现要在这4名学生中随机选取2名学生参加学校的阅读分享沙龙,请用列举法(画树状图或列表)求所选取的这2名学生恰好性别相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节期间,某品牌粽子经销商销售甲、乙两种不同味道的粽子,已知一个甲种粽子和一个乙种粽子的进价之和为10元,每个甲种粽子的利润是4元,每个乙种粽子的售价比其进价的2倍少1元,小王同学买4个甲种粽子和3个乙种粽子一共用了61元.
(1)甲、乙两种粽子的进价分别是多少元?
(2)在(1)的前提下,经销商统计发现:平均每天可售出甲种粽子200个和乙种粽子150个.如果将两种粽子的售价各提高1元,则每天将少售出50个甲种粽子和40个乙种粽子.为使每天获取的利润更多,经销商决定把两种粽子的价格都提高x元.在不考虑其他因素的条件下,当x为多少元时,才能使该经销商每天销售甲、乙两种粽子获取的利润为1190元?
查看答案和解析>>
科目:初中数学 来源: 题型:
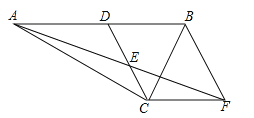
【题目】如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.
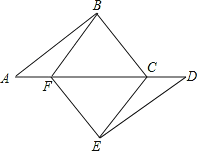
(1)求证:四边形BCEF是平行四边形,
(2)若∠ABC=90°,AB=4,BC=3,当AF为何值时,四边形BCEF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
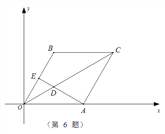
【题目】在如图直角坐标系内,四边形AOBC是边长为2的菱形,E为边OB的中点,连结AE与对角线OC交于点D,且∠BCO=∠EAO,则点D坐标为( )
A. (![]() ,
,![]() ) B. (1,
) B. (1,![]() ) C. (
) C. (![]() ,
,![]() ) D. (1,
) D. (1,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com