
【题目】计算(直接写出结果)
(1)-4-3=
(2)13-(-3)=
(3)-8+(-2)=
(4)![]() ×(-1)=
×(-1)=
(5)-(-1![]() )2=
)2=
(6)![]() ÷(-2)=
÷(-2)=
(7)(-3)4×0=
(8)-1.2×![]() =
=
(9)|+7|-|-5|=
【答案】(1)-7;(2)16;(3)-10;(4)![]() ;(5)
;(5)![]() ;(6)
;(6)![]() ;(7)0;(8)0.12;(9)2
;(7)0;(8)0.12;(9)2
【解析】
(1)(2)原式利用减法法则计算即可得到结果;
(3)原式利用加法法则,计算即可得到结果;
(4)原式利用乘法法则,计算即可得到结果;;
(5)原式利用乘方的意义计算即可得到结果;
(6)原式利用除法法则计算即可得到结果;
(7)原式利用0乘以任何数结果为0,计算即可;
(8)原式利用同号两数相乘的法则计算即可得到结果;
(9)原式先计算绝对值运算,再计算加法运算即可.
解:(1)原式= -3+(-4)=-7;
(2)原式=13+3=16;
(3)原式=-(8+2)=-10;
(4)原式=![]() ×1=
×1=![]() ;
;
(5)原式= -![]() =
=![]() ;
;
(6)原式= -![]() =
=![]() ;
;
(7)原式=0;
(8)原式=1.2×![]() =0.12;
=0.12;
(9)原式=7-5=2.


科目:初中数学 来源: 题型:
【题目】在矩形![]() 中,
中,![]() ,
,![]() ,将
,将![]() 沿着对角线
沿着对角线![]() 对折得到
对折得到![]() .
.
(1)如图,![]() 交
交![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,求
,求![]() 的长.
的长.
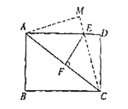
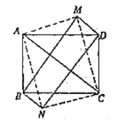
(2)如图,再将![]() 沿着对角线
沿着对角线![]() 对折得到
对折得到![]() ,顺次连接
,顺次连接![]() 、
、![]() 、
、![]() 、
、![]() ,求:四边形
,求:四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了开展“阳光体育运动”,计划购买篮球与足球共![]() 个,已知每个篮球的价格为
个,已知每个篮球的价格为![]() 元,每个足球的价格为
元,每个足球的价格为![]() 元
元
(1)若购买这两类球的总金额为![]() 元,求篮球和足球各购买了多少个?
元,求篮球和足球各购买了多少个?
(2)元旦期间,商家给出蓝球打九折,足球打八五折的优惠价,若购买这种篮球与足球各![]() 个,那么购买这两类球一共需要多少钱?
个,那么购买这两类球一共需要多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
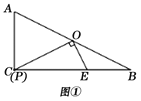
【题目】已知:在Rt△ABC中,∠ACB=90°,AC=4,BC=8,O是AB边的中点,P是AC边上的动点,OE⊥OP交BC边于点E,连接PE.
(1)如图①,当P与C重合时,线段PE的长为___________;
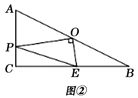
(2)如图②,当P在AC边上运动时,
①探究:线段PA,PE,EB之间的数量关系,并证明你的结论;
②若设PA=![]() ,PE2=y,求y与x之间的函数关系式及线段PE的最小值.
,PE2=y,求y与x之间的函数关系式及线段PE的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某检修小组乘一辆汽车沿一条东西向公路检修线路,约定向东为正,某天从地出发到收工时,行走记录如下:(单位:![]() )+15,-2,+5,-3,+8,-3,-1,+11,+4,-5,-2,+7,-3,+5
)+15,-2,+5,-3,+8,-3,-1,+11,+4,-5,-2,+7,-3,+5
(1)请问:收工时检修小组距离![]() 有多远?在
有多远?在![]() 地的哪一边?
地的哪一边?
(2)若检修小组所乘的汽车每一百千米平均耗油8升,则汽车从![]() 地出发到收工大约耗油多少升?
地出发到收工大约耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电动车厂一周计划生产2100辆电动车,平均每天计划生产300辆,由于各种原因,实际每天的生产量与计划量相比有出入.下表是某周的生产情况(超产为正,减产为负).
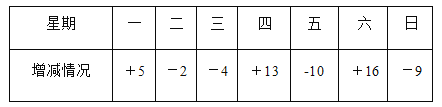
(1)根据记录可知本周前三天共生产电动车多少辆?
(2)本周产量最多的一天比产量最少的一天多生产电动车多少辆?
(3)该厂实行每周计件工资制,每生产一辆电动车可得a元,若超额完成,则超额部分每辆再奖b元(b<a),少生产一辆扣b元,求该厂工人这一周的工资总额.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年5月19日为第29个“全国助残日”.我市某中学组织了献爱心捐款活动,该校数学课外活动小组对本次捐款活动做了一次抽样调查,并绘制了如下不完整的频数分布表和频数分布直方图(每组含前一个边界,不含后一个边界).

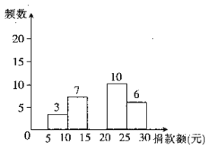
(1)填空:![]() _________,
_________,![]() _________.
_________.
(2)补全频数分布直方图.
(3)该校有2000名学生,估计这次活动中爱心捐款额在![]() 的学生人数.
的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
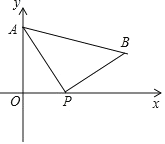
【题目】如图,A(0,4)是直角坐标系 y 轴上一点,动点 P 从原点 O 出发,沿 x 轴正半轴运动,速度为每秒 1 个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为 t 秒.
(1)若 AB∥x 轴,求 t 的值;
(2)若OP=![]() OA,求B点的坐标.
OA,求B点的坐标.
(3)当 t=3 时,x 轴上是否存在有一点 M,使得以 M、P、A 为顶点的三角形是等腰三角形,请直接写出点 M 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知自行车与摩托车从甲地开往乙地,OA与BC分别表示它们与甲地距离s(千米)与时间t(小时)的关系,则:
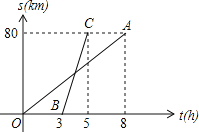
(1)摩托车每小时走 千米,自行车每小时走 千米;
(2)自行车出发后多少小时,它们相遇?
(3)摩托车出发后多少小时,他们相距10千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com