
【题目】在矩形![]() 中,
中,![]() ,
,![]() ,将
,将![]() 沿着对角线
沿着对角线![]() 对折得到
对折得到![]() .
.
(1)如图,![]() 交
交![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,求
,求![]() 的长.
的长.
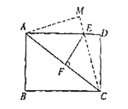
(2)如图,再将![]() 沿着对角线
沿着对角线![]() 对折得到
对折得到![]() ,顺次连接
,顺次连接![]() 、
、![]() 、
、![]() 、
、![]() ,求:四边形
,求:四边形![]() 的面积.
的面积.
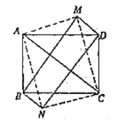
【答案】(1)![]() ;(2)
;(2)![]() 的面积是
的面积是![]() .
.
【解析】
(1)由矩形的性质可得AB=CD=3,AD=BC=4,∠B=∠D=90°,AD∥BC,由勾股定理可求AC=5,由折叠的性质和平行线的性质可得AE=CE,由勾股定理可求AE的长,由三角形面积公式可求EF的长;
(2)由折叠的性质可得AB=AM=3,CD=CN=3,∠BAC=∠CAM,∠ACD=∠ACN,AC⊥DN,DF=FN,由“SAS”可证△BAM≌△DCN,△AMD≌△CNB可得
MD=BN,BM=DN,可得四边形MDNB是平行四边形,通过证明四边形MDNB是矩形,可得∠BND=90°,由三角形面积公式可求DF的长,由勾股定理可求BN的长,即可求四边形BMDN的面积.
解:(1)∵四边形ABCD是矩形
∴AB=CD=3,AD=BC=4,∠B=∠D=90°,AD∥BC
∴AC=![]() =5,
=5,
∵将Rt△ABC沿着对角线AC对折得到△AMC.
∴∠BCA=∠ACE,
∵AD∥BC
∴∠DAC=∠BCA
∴∠EAC=∠ECA
∴AE=EC
∵EC2=ED2+CD2,
∴AE2=(4AE)2+9,
∴AE=![]() ,
,
∵S△AEC=![]() ×AE×DC=
×AE×DC=![]() ×AC×EF,
×AC×EF,
∴![]() ×3=5×EF,
×3=5×EF,
∴EF=![]() ;
;
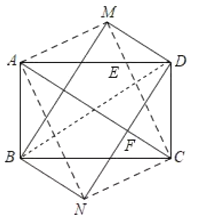
(2)如图所示:
∵将Rt△ABC沿着对角线AC对折得到△AMC,将Rt△ADC沿着对角线AC对折得到△ANC,
∴AB=AM=3,CD=CN=3,∠BAC=∠CAM,∠ACD=∠ACN,AC⊥DN,DF=FN,
∵AB∥CD
∴∠BAC=∠ACD
∴∠BAC=∠ACD=∠CAM=∠ACN
∴∠BAM=∠DCN,且BA=AM=CD=CN
∴△BAM≌△DCN(SAS)
∴BM=DN
∵∠BAM=∠DCN
∴∠BAM90°=∠DCN90°
∴∠MAD=∠BCN,且AD=BC,AM=CN
∴△AMD≌△CNB(SAS)
∴MD=BN,且BM=DN
∴四边形MDNB是平行四边形
连接BD,
由1)可知:∠EAC=∠ECA,
∵∠AMC=∠ADC=90°
∴点A,点C,点D,点M四点共圆,
∴∠ADM=∠ACM,
∴∠ADM=∠CAD
∴AC∥MD,且AC⊥DN
∴MD⊥DN,
∴四边形BNDM是矩形
∴∠BND=90°
∵S△ADC=![]() ×AD×CD=
×AD×CD=![]() ×AC×DF
×AC×DF
∴DF=![]()
∴DN=![]()
∵四边形ABCD是矩形
∴AC=BD=5,
∴BN=![]()
∴四边形BMDN的面积=BN×DN=![]() ×
×![]() =
=![]() .
.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】学习了统计知识后,小亮的数学老师要求每个学生就本班同学的上学方式进行一次调查统计,下图是小亮通过收集整理数据后绘制的两幅不完整的统计图,请根据图中提供的信息,解答下列问题:


(1)该班共有________名学生;
(2)将“骑自行车”部分的条形统计图补充完整;
(3)在扇形统计图中,求出“乘车”部分所对应的圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场对一种新售的手机进行市场问卷调查,其中一个项目是让每个人按A(不喜欢)、B(一般)、C(不比较喜欢)、D(非常喜欢)四个等级对该手机进行评价,图①和图②是该商场采集数据后,绘制的两幅不完整的统计图,请你根据以上统计图提供的信息,回答下列问题:
(1)本次调查的人数为多少人?A等级的人数是多少?请在图中补全条形统计图.
(2)图①中,a等于多少?D等级所占的圆心角为多少度?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E是 BC边的中点,点B′与点B关于AE对称,BB′与AE交于点F.下列结论错误的是( )

A. AB′=AD B. ∠ADB′=75°
C. ∠CB′D=135° D. △FCB′是等腰直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图,用同样规格的黑白两色正方形瓷砖铺设矩形地面,请观察图形,并探究下列问题:
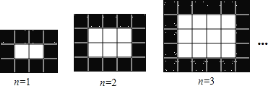
![]() 在第
在第![]() 个图中,共有白色瓷砖________块;在第
个图中,共有白色瓷砖________块;在第![]() 个图中,共有白色瓷砖________块;
个图中,共有白色瓷砖________块;
![]() 在第
在第![]() 个图中,共有瓷砖________块;在第
个图中,共有瓷砖________块;在第![]() 个图中,共有瓷砖________块;
个图中,共有瓷砖________块;
![]() 如果每块黑瓷砖
如果每块黑瓷砖![]() 元,白瓷砖
元,白瓷砖![]() 元,铺设当
元,铺设当![]() 时,共需花多少钱购买瓷砖?
时,共需花多少钱购买瓷砖?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列菱形的摆放规律,解答下列问题.
(1)如图:
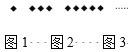
按此规律,图4有____个菱形,若第![]() 个图形有35个菱形,则
个图形有35个菱形,则![]() ___________;
___________;
(2)如图:

按此规律,图5有______个菱形,若第![]() 个图形有___个菱形(用含
个图形有___个菱形(用含![]() 的式子表示).
的式子表示).
(3)如图:
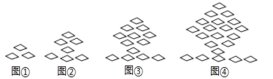
按此规律图6有________个菱形,第![]() 个图形中有__________个菱形(用含的式子表示).
个图形中有__________个菱形(用含的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
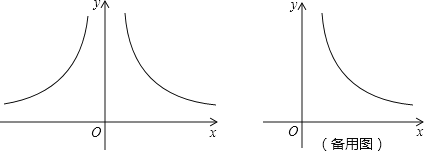
【题目】平面直角坐标系xOy中,点A、B分别在函数y1=![]() (x>0),与y2=﹣
(x>0),与y2=﹣![]() (x<0)的图象上,A、B的横坐标分别为a、b.(a、b为任意实数)
(x<0)的图象上,A、B的横坐标分别为a、b.(a、b为任意实数)
(1)若AB∥x轴,求△OAB的面积;
(2)作边长为2的正方形ACDE,使AC∥x轴,点D在点A的左上方,那么,当a≥3时,CD边与函数y1=![]() (x>0)的图象有交点,请说明理由.
(x>0)的图象有交点,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算(直接写出结果)
(1)-4-3=
(2)13-(-3)=
(3)-8+(-2)=
(4)![]() ×(-1)=
×(-1)=
(5)-(-1![]() )2=
)2=
(6)![]() ÷(-2)=
÷(-2)=
(7)(-3)4×0=
(8)-1.2×![]() =
=
(9)|+7|-|-5|=
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com