
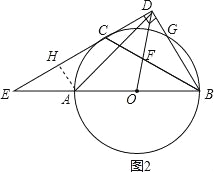
【题目】如图,AB是⊙O的直径,C、G是⊙O上两点,且C是弧AG的中点,过点C的直线CD⊥BG的延长线于点D,交BA的延长线于点E,连接BC,交OD于点F.

(1)求证:CD是⊙O的切线;
(2)若![]() ,求证:AE=AO;
,求证:AE=AO;
(3)连接AD,在(2)的条件下,若CD=2![]() ,求AD的长.
,求AD的长.
【答案】(1)证明见解析(2)∠E=30°;(3)![]()
【解析】
试题分析:(1)如图1,连接OC,AC,CG,由圆周角定理得到∠ABC=∠CBG,根据同圆的半径相等得到OC=OB,于是得到∠OCB=∠OBC,等量代换得到∠OCB=∠CBG,根据平行线的判定得到OC∥BG,即可得到结论;
(2)由OC∥BD,得到△OCF∽△BDF,△EOC∽△EBD,得到![]() ,
,![]() ,根据直角三角形的性质即可得到结论;
,根据直角三角形的性质即可得到结论;
(3)如图2,过A作AH⊥DE于H,解直角三角形得到BD=6,DE=6![]() ,BE=12,在Rt△DAH中,AD=
,BE=12,在Rt△DAH中,AD=![]() ,求出答案即可.
,求出答案即可.
试题解析:(1)如图1,连接OC,AC,CG,
∵AC=CG,
∴![]() ,
,
∴∠ABC=∠CBG,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠OCB=∠CBG,
∴OC∥BG,
∵CD⊥BG,
∴OC⊥CD,
∴CD是⊙O的切线;

(2)∵OC∥BD,
∴△OCF∽△BDF,△EOC∽△EBD,
∴![]() ,
,
∴![]() ,
,
∵OA=OB,
∴AE=OA=OB,
∴OC=![]() OE,
OE,
∵∠ECO=90°,
∴∠E=30°;
(3)如图2,过A作AH⊥DE于H,
∵∠E=30°
∴∠EBD=60°,
∴∠CBD=![]() ∠EBD=30°,
∠EBD=30°,
∵CD=2![]() ,
,
∴BD=6,DE=6![]() ,BE=12,
,BE=12,
∴AE=![]() BE=4,
BE=4,
∴AH=2,
∴EH=2![]() ,
,
∴DH=4![]() ,
,
在Rt△DAH中,AD=![]() =2
=2![]() .
.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
【题目】如图,OA的方向是北偏东15°,OB的方向是西偏北50度.
(1)若∠AOC=∠AOB,则OC的方向是;
(2)OD是OB的反向延长线,OD的方向是;
(3)∠BOD可看作是OB绕点O逆时针方向至OD,作∠BOD的平分线OE,OE的方向是;
(4)在(1)、(2)、(3)的条件下,∠COE= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察图,解答下列问题.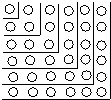
(1)图中的小圆圈被折线隔开分成六层,第一层有1个小圆圈,第二层有3个圆圈,第三层有5个圆圈,…,第六层有11个圆圈.如果要你继续画下去,那么第八层有几个小圆圈?第n层呢?
(2)某一层上有65个圆圈,这是第几层?
(3)数图中的圆圈个数可以有多种不同的方法.
比如:前两层的圆圈个数和为(1+3)或22 ,
由此得,1+3=22 .
同样,
由前三层的圆圈个数和得:1+3+5=32 .
由前四层的圆圈个数和得:1+3+5+7=42 .
由前五层的圆圈个数和得:1+3+5+7+9=52 .
…
根据上述请你猜测,从1开始的n个连续奇数之和是多少?用公式把它表示出来.
(4)计算:1+3+5+…+99的和;
(5)计算:101+103+105+…+199的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,OC是∠AOD的平分线,OE是∠BOD的平分线.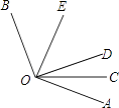
(1)如果∠AOB=150°,求∠COE的度数;
(2)如果∠AOB=120°,那么∠COE=;
(3)如果∠AOB=α,那么∠COE= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师在黑板上出了一道解方程的题 ![]() =1﹣
=1﹣ ![]() ,小明马上举起了手,要求到黑板上去做,他是这样做的:
,小明马上举起了手,要求到黑板上去做,他是这样做的:
4(2x﹣1)=1﹣3(x+2)①
8x﹣4=1﹣3x﹣6 ②
8x+3x=1﹣6+4 ③
11x=﹣1 ④![]() ⑤
⑤
老师说:小明解一元一次方程的一般步骤都掌握了,但解题时有一步做错了,请你指出他错在第步(填编号),错误的原因是;然后,你自己细心地解下列方程: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com