
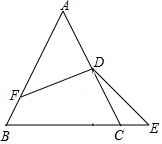
 已知△ABC是等边三角形,D是AC的中点,F为AB边上一点,且AF=2BF,E为射线BC上一点,∠EDF=120°,则$\frac{CE}{CD}$=$\frac{1}{3}$.
已知△ABC是等边三角形,D是AC的中点,F为AB边上一点,且AF=2BF,E为射线BC上一点,∠EDF=120°,则$\frac{CE}{CD}$=$\frac{1}{3}$. 分析 过D作DG∥BC交AB于G,则DG为△ABC的中位线,根据等边三角形的性质得∠ACB=∠ABC=60°,由DG∥BC,得∠FGD=120°,∠GDC=120°,△AGD为等边三角形,而∠EDF=120°,得∠GDF=∠CDE,易证得△GDF∽△CDE,所以FG:CE=DG:DC,即CE:DC=FG:DG=FG:AG,当AF=2BF,设BF=x,AF=2x,则AB=3x,AG=1.5x,FG=1.5x-x=0.5x,即可得到CE:DC的比值.
解答 解:过D作DG∥BC交AB于G,如图1,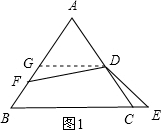
∵D是AC的中点,
∴DG为△ABC的中位线,
∵△ABC是等边三角形,
∴∠ACB=∠ABC=60°,
∴∠DCE=120°,
又∵DG∥BC,
∴∠FGD=120°,∠GDC=120°,△AGD为等边三角形,
而∠EDF=120°,
∴∠GDF=∠CDE,
∴△GDF∽△CDE,
∴FG:CE=DG:DC,即CE:DC=FG:DG,
而DG=AG=BG,AF=2BF,
设BF=x,AF=2x,则AB=3x,AG=1.5x,FG=1.5x-x=0.5x,
∴CE:DC=FG:DG=FG:AG=1.5x:0.5x=1:3.
故答案为:$\frac{1}{3}$.
点评 本题考查了等边三角形的性质:等边三角形三边相等;三个角都等于60°;也考查了相似三角形的判定与性质以及含30度的直角三角形三边的关系.


 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
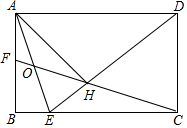 如图,在矩形ABCD中,BC=$\sqrt{2}$AB,∠ADC的平分线交边BC于点E,AH⊥DE于点H,连接CH并延长交边AB于点F,连接AE交CF于点O,给出下列命题:
如图,在矩形ABCD中,BC=$\sqrt{2}$AB,∠ADC的平分线交边BC于点E,AH⊥DE于点H,连接CH并延长交边AB于点F,连接AE交CF于点O,给出下列命题:| A. | (1)(2)(3) | B. | (2)(3)(4) | C. | (2)(4) | D. | (1)(3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 环岛是为了减少车辆行驶冲突,在多个交通路口交汇的地方设置的交通设施,多为圆形,它使车辆按统一方向行驶,将冲突点转变为通行点,能有效地减少交通事故的发生,如图是该交通环岛的简化模型(因路段FG施工,禁止从路段EF行驶过来的车辆在环岛内通行,只能往环岛外行驶),某时段内该交通环岛的进出机动车辆数如图所示,图中箭头方向表示车辆的行驶方向.
环岛是为了减少车辆行驶冲突,在多个交通路口交汇的地方设置的交通设施,多为圆形,它使车辆按统一方向行驶,将冲突点转变为通行点,能有效地减少交通事故的发生,如图是该交通环岛的简化模型(因路段FG施工,禁止从路段EF行驶过来的车辆在环岛内通行,只能往环岛外行驶),某时段内该交通环岛的进出机动车辆数如图所示,图中箭头方向表示车辆的行驶方向.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com