
 的度数.
的度数.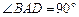 ,
,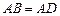 ,点M,N是BD边上的任意两点,且
,点M,N是BD边上的任意两点,且 ,将△ABM绕点A逆时针旋转
,将△ABM绕点A逆时针旋转 至△ADH位置,连接
至△ADH位置,连接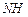 ,试判断MN,ND,DH之间的数量关系,并说明理由.
,试判断MN,ND,DH之间的数量关系,并说明理由. ,
, ,
, ,求AG,MN的长.
,求AG,MN的长.

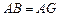 ,
,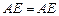 ,
,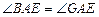 .················································· 1分
.················································· 1分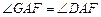 .
.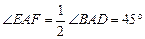 .······································································ 2分
.······································································ 2分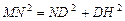 .······································································ 3分
.······································································ 3分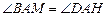 ,
,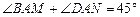 ,
,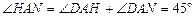 . ∴
. ∴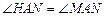 .
.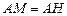 ,
,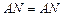 ,
,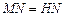 .························································· 5分
.························································· 5分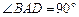 ,
,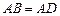 ,
,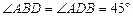 . ∴
. ∴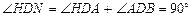 .
. . ∴
. ∴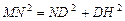 .···································· 6分
.···································· 6分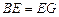 ,
,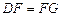 .
.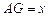 ,则
,则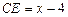 ,
,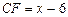 .
.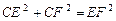 ,
,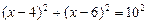 .
.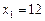 ,
,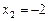 (舍去负根).
(舍去负根).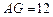 .························································································· 8分
.························································································· 8分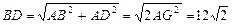 .
.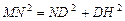 ,
,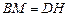 ,
,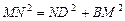 .·········································································· 9分
.·········································································· 9分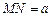 ,则
,则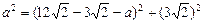 .
.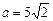 .即
.即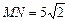 .···································································· 10分
.···································································· 10分

科目:初中数学 来源:不详 题型:解答题
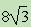 ,求AC的长.
,求AC的长.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
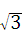 ,点O是AB的中点,点P在AB的延长线上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点发发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).
,点O是AB的中点,点P在AB的延长线上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点发发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 .
.
|
 ?若存在,请求出该点坐标,若不存在,请说明理由.
?若存在,请求出该点坐标,若不存在,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com