
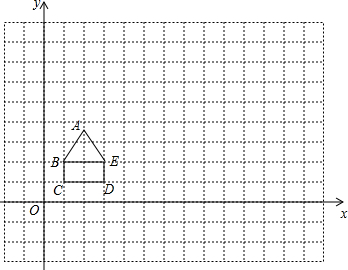
分析 (1)首先过点A作AF⊥BE,由△ABE是等边三角形,可求得AF的长,继而可求得E点和A点的坐标;
(2)首先根据题意画出图形,由位似图形的性质即可求得各对应点的坐标.
解答 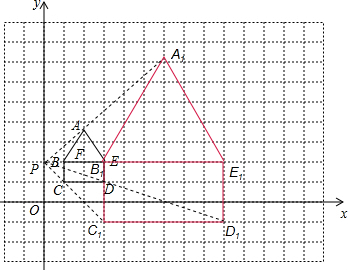 解:(1)过点A作AF⊥BE,
解:(1)过点A作AF⊥BE,
∵△ABE是等边三角形,
∴AB=BE=2,∠ABE=60°,
∴AF=AB•sin60°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
∴点A的坐标为:(2,2+$\sqrt{3}$),点E的坐标为:(3,2);
(2)如图:A1(6,2+3$\sqrt{3}$),B1(3,2),C1(3,-1),D1(9,-1),E1(9,2).
点评 此题考查了位似图形的性质与矩形、等边三角形的性质.注意作位似图形时找准位似中心与位似比.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
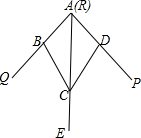 如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC.将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( )
如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC.将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( )| A. | SAS | B. | ASA | C. | AAS | D. | SSS |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小敏上午8:00从家里出发,骑车去一家超市购物,然后从这家超市返回家中.小敏离家的路程y(米)和所经过的时间x(分)之间的函数图象如图所示.请根据图象回答下列问题:
小敏上午8:00从家里出发,骑车去一家超市购物,然后从这家超市返回家中.小敏离家的路程y(米)和所经过的时间x(分)之间的函数图象如图所示.请根据图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 20<m<24 | B. | 4<m<44 | C. | 2<m<22 | D. | 10<m<12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com