
【题目】在一次夏令营活动中,小明同学从营地![]() 出发,要到
出发,要到![]() 地的北偏东
地的北偏东![]() 方向的
方向的![]() 处,他先沿正东方向走到
处,他先沿正东方向走到![]() 地,再沿北偏东
地,再沿北偏东![]() 方向走,恰能到达目的地
方向走,恰能到达目的地![]() ,已知
,已知![]() ,
,![]() 两地相距
两地相距![]() ,由此可知,
,由此可知,![]() ,
,![]() 两地相距________
两地相距________![]() .
.
科目:初中数学 来源: 题型:
【题目】(本题8分)如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
(1)求证:△ABC≌△AED;
(2)当∠B=140°时,求∠BAE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】过三角形一个顶点的直线,把原三角形分割成两个三角形,要求分得的两个三角形中至少有一个是等腰三角形.
(1)如果原三角形是顶点为108°的等腰三角形,这样的直线有________条.
(2)如果原三角形是等腰直角三角形,这样的直线有________条.
(3)如果原三角形是有一个锐角是30°的直角三角形,这样的直线有________条.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某草莓采摘园元旦至春节期间推出了甲、乙两种优惠方案.
甲种优惠方案:游客进园需要购买40元的门票(每个家庭购买一张门票),采摘的草莓均按定价的六折卖给采摘游客;
乙种优惠方案:游客进园不需购买门票,采摘的草莓按定价出售,但超过一定重量后,超过的部分打折卖给采摘的游客.
优惠期间,设某游客(或一个家庭)采摘草莓的重量为x(kg),选用甲种优惠方案采摘所需的总费用为y1(元),选用乙种优惠方案采摘所需的总费用为y2(元).已知1,y2与采摘重量x(kg)之间的函数关系如图所示.
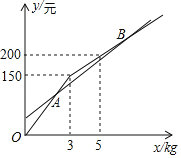
(1)分别求y1,y2与x之间的函数关系式;
(2)求点A的坐标,并解释坐标的实际意义;
(3)采摘重量x为多少时,游客选用甲种优惠方案采摘更合算.(直接写出答案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店销售一种水果的成本价是![]() 元/千克.在销售过程中发现,当这种水果的价格定在
元/千克.在销售过程中发现,当这种水果的价格定在![]() 元/千克时,每天可以卖出
元/千克时,每天可以卖出![]() 千克.在此基础上,这种水果的单价每提高
千克.在此基础上,这种水果的单价每提高![]() 元/千克,该水果店每天就会少卖出
元/千克,该水果店每天就会少卖出![]() 千克.
千克.
![]() 若该水果店每天销售这种水果所获得的利润是
若该水果店每天销售这种水果所获得的利润是![]() 元,则单价应定为多少?
元,则单价应定为多少?
![]() 在利润不变的情况下,为了让利于顾客,单价应定为多少?
在利润不变的情况下,为了让利于顾客,单价应定为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() (其中m>0)与x轴分别交于A,B两点(A在B的右侧),与y轴交于点c.
(其中m>0)与x轴分别交于A,B两点(A在B的右侧),与y轴交于点c.
(1)求△AOC的周长,(用含m的代数式表示)
(2)若点P为直线AC上的一点,且点P在第二象限,满足OP2=PCPA,求tan∠APO的值及用含m的代数式表示点P的坐标;
(3)在(2)的情况下,线段OP与抛物线相交于点Q,若点Q恰好为OP的中点,此时对于在抛物线上且介于点C与抛物线顶点之间(含点C与顶点)的任意一点M(x0,y0)总能使不等式n≤![]() 及不等式2n﹣
及不等式2n﹣![]() 恒成立,求n的取值范围.
恒成立,求n的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从6 月30日起,某县普降特大暴雨,遭受了短期降水量最大、内河水位历史最高、防汛压力最重的百年不遇的灾害.洪水无情人有情,该县实验学校9 (1)班计划用捐款从商店购买同品牌的雨衣和雨伞送往抗洪前线.已知购买一件雨衣比购买一把雨伞多用![]() 元,若用
元,若用![]() 元购买雨衣和用
元购买雨衣和用![]() 元购买雨伞,则购买雨衣的件数是购买雨伞把数的一半.
元购买雨伞,则购买雨衣的件数是购买雨伞把数的一半.
(1)求购买该品牌的一件雨衣、一把雨伞各需要多少元.
(2)经商谈,商店给予该班级购买一件该品牌的雨衣赠送把该品牌的雨伞的优惠, 如果该班需要购买雨伞个数是雨衣件数的![]() 倍还多
倍还多![]() 个,且该班购买雨衣和雨伞的总费用不超过
个,且该班购买雨衣和雨伞的总费用不超过![]() 元,那么该班最多可以购买多少件该品牌的雨衣?
元,那么该班最多可以购买多少件该品牌的雨衣?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com