
【题目】某草莓采摘园元旦至春节期间推出了甲、乙两种优惠方案.
甲种优惠方案:游客进园需要购买40元的门票(每个家庭购买一张门票),采摘的草莓均按定价的六折卖给采摘游客;
乙种优惠方案:游客进园不需购买门票,采摘的草莓按定价出售,但超过一定重量后,超过的部分打折卖给采摘的游客.
优惠期间,设某游客(或一个家庭)采摘草莓的重量为x(kg),选用甲种优惠方案采摘所需的总费用为y1(元),选用乙种优惠方案采摘所需的总费用为y2(元).已知1,y2与采摘重量x(kg)之间的函数关系如图所示.
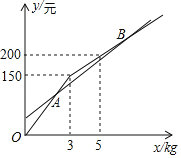
(1)分别求y1,y2与x之间的函数关系式;
(2)求点A的坐标,并解释坐标的实际意义;
(3)采摘重量x为多少时,游客选用甲种优惠方案采摘更合算.(直接写出答案即可)
【答案】(1)y1=30x+40;当0≤x≤3时,y2=50x;当x>3时,y2=25x+75;(2)实际意义是当采摘重量为2kg时,两种优惠方案的总费用都为100元;(3)当采摘重量为2<x<7时,游客选用甲种方案更合算.
【解析】
(1)根据乙种优惠方案图象可知:不优惠采摘3千克草莓需150元,即可求出采摘园优惠前的草莓每千克定价,根据题意即可写y1与x之间的函数关系式,然后根据x的取值范围分类讨论,分别用待定系数法求出y2与x之间的函数关系式即可;
(2)将y1与x的关系式和OA的关系式联立即可求出点A的坐标,根据点A的横坐标和纵坐标的实际意义即可解答;
(3)将y1=30x+40和y2=25x+75联立即可求出点B的坐标,然后根据图象可知在点A和点B之间时,y1<y2,从而得出结论.
(1)采摘园优惠前的草莓每千克定价为![]() (元).
(元).
由题意,得y1=50×0.6x+40=30x+40.
当0≤x≤3时,设y2=kx,根据题意,得150=3k.解得k=50.
∵y2=50x;
当x>3时,设y2=kx+b,由题意知y2=kx+b的图象过点将(3,150)和(5,200),
则![]() ,解得
,解得![]() ,
,
∴y2=25x+75.
∴y2=![]() ;
;
(2)根据题意,得![]()
解得![]()
则点A的坐标为(2,100).
实际意义是当采摘重量为2kg时,两种优惠方案的总费用都为100元.
(3)将y1=30x+40和y2=25x+75联立,得![]()
解得:![]()
则点B的坐标为(7,250)
由图象可知:在点A和点B之间时,y1<y2
∴当采摘重量为2<x<7时,游客选用甲种方案更合算.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案科目:初中数学 来源: 题型:
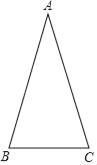
【题目】如图,在△ABC中,AB=AC,点D在AB边上,点D到点A的距离与点D到点C的距离相等.
(1)利用尺规作图作出点D,不写作法但保留作图痕迹.
(2)若△ABC的底边长5,周长为21,求△BCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABE≌△ACD,且AB=AC.
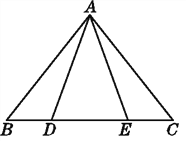
(1)说明△ABE经过怎样的变换后可与△ACD重合.
(2)∠BAD与∠CAE有何关系?请说明理由.
(3)BD与CE相等吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90,点D、E分别是边AB、AC的中点,延长DE至F,使得AF//CD,连接BF、CF。求证:四边形AFCD是菱形。
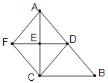
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,AD=4,CD=10,P是AB上一动点,M、N、E分别是PD、PC、CD的中点.
(1)求证:四边形PMEN是平行四边形;
(2)请直接写出当AP为何值时,四边形PMEN是菱形;
(3)四边形PMEN有可能是矩形吗?若有可能,求出AP的长;若不可能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次夏令营活动中,小明同学从营地![]() 出发,要到
出发,要到![]() 地的北偏东
地的北偏东![]() 方向的
方向的![]() 处,他先沿正东方向走到
处,他先沿正东方向走到![]() 地,再沿北偏东
地,再沿北偏东![]() 方向走,恰能到达目的地
方向走,恰能到达目的地![]() ,已知
,已知![]() ,
,![]() 两地相距
两地相距![]() ,由此可知,
,由此可知,![]() ,
,![]() 两地相距________
两地相距________![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 的一元二次方程x2-(k+2)x+k-1=0
的一元二次方程x2-(k+2)x+k-1=0
(1)若方程的一个根为 -1,求![]() 的值和方程的另一个根;
的值和方程的另一个根;
(2)求证:不论![]() 取何值,该方程都有两个不相等的实数根.
取何值,该方程都有两个不相等的实数根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com