
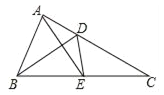
【题目】如图,将△ABC沿角平分线BD所在直线翻折,顶点A恰好落在边BC的中点E处,AE=BD,那么tan∠ABD=( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
作CM⊥AE交AE的延长线于M,作DN⊥AB于N,DF⊥BC于F,AE与BD交于点K,设DK=a,先证明AD:CD=1:2,再证明△BKE≌△CME,得BK=CM=3a,根据tan∠ABD=![]() 即可解决问题.
即可解决问题.
如图,作CM⊥AE交AE的延长线于M,作DN⊥AB于N,DF⊥BC于F,AE与BD交于点K,设DK=a.
∵AB=BE=EC,∴BC=2AB.
∵DB平分∠ABC,∴DN=DF.
∵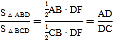 ,∴
,∴![]() .
.
∵AB=FB,∠ABD=∠EBD,∴DB⊥AM,AK=KE.
∵DB⊥AM,CM⊥AM,∴DK∥CM,∴![]() ,∠KBE=∠MCE,∴CM=3a.在△BKE和△CME中,
,∠KBE=∠MCE,∴CM=3a.在△BKE和△CME中,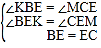 ,∴△BKE≌△CME,∴BK=CM=3a,∴BD=AE=4a,∴AK=KE=2a,∴tan∠ABD=
,∴△BKE≌△CME,∴BK=CM=3a,∴BD=AE=4a,∴AK=KE=2a,∴tan∠ABD=![]() .
.
故选B.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l的函数表达式为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径画圆,交直线l于点
为半径画圆,交直线l于点![]() ,交x轴正半轴于点
,交x轴正半轴于点![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径画圆,交直线l于点
为半径画圆,交直线l于点![]() ,交x轴正半轴于点
,交x轴正半轴于点![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径画圆,交直线l于点
为半径画圆,交直线l于点![]() ,交x轴正半轴于点
,交x轴正半轴于点![]() ;
;![]() 按此做法进行下去,其中
按此做法进行下去,其中![]() 的长为______.
的长为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某草莓采摘园元旦至春节期间推出了甲、乙两种优惠方案.
甲种优惠方案:游客进园需要购买40元的门票(每个家庭购买一张门票),采摘的草莓均按定价的六折卖给采摘游客;
乙种优惠方案:游客进园不需购买门票,采摘的草莓按定价出售,但超过一定重量后,超过的部分打折卖给采摘的游客.
优惠期间,设某游客(或一个家庭)采摘草莓的重量为x(kg),选用甲种优惠方案采摘所需的总费用为y1(元),选用乙种优惠方案采摘所需的总费用为y2(元).已知1,y2与采摘重量x(kg)之间的函数关系如图所示.
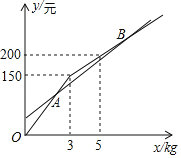
(1)分别求y1,y2与x之间的函数关系式;
(2)求点A的坐标,并解释坐标的实际意义;
(3)采摘重量x为多少时,游客选用甲种优惠方案采摘更合算.(直接写出答案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店销售一种水果的成本价是![]() 元/千克.在销售过程中发现,当这种水果的价格定在
元/千克.在销售过程中发现,当这种水果的价格定在![]() 元/千克时,每天可以卖出
元/千克时,每天可以卖出![]() 千克.在此基础上,这种水果的单价每提高
千克.在此基础上,这种水果的单价每提高![]() 元/千克,该水果店每天就会少卖出
元/千克,该水果店每天就会少卖出![]() 千克.
千克.
![]() 若该水果店每天销售这种水果所获得的利润是
若该水果店每天销售这种水果所获得的利润是![]() 元,则单价应定为多少?
元,则单价应定为多少?
![]() 在利润不变的情况下,为了让利于顾客,单价应定为多少?
在利润不变的情况下,为了让利于顾客,单价应定为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般成年人的脚长(厘米)与鞋码(码)有如下关系:
脚长 | 23 | 23.5 | 24 | 24.5 | … |
鞋码 | 36 | 37 | 38 | 39 | … |
(1)若某人的脚长为26厘米,他应穿多少码的鞋?
(2)请建立鞋码![]() (厘米)与脚长
(厘米)与脚长![]() (码)之间的函数表达式;
(码)之间的函数表达式;
(3)我国著名篮球运动员姚明穿53码的鞋,请你根据以上关系计算他的脚长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() (其中m>0)与x轴分别交于A,B两点(A在B的右侧),与y轴交于点c.
(其中m>0)与x轴分别交于A,B两点(A在B的右侧),与y轴交于点c.
(1)求△AOC的周长,(用含m的代数式表示)
(2)若点P为直线AC上的一点,且点P在第二象限,满足OP2=PCPA,求tan∠APO的值及用含m的代数式表示点P的坐标;
(3)在(2)的情况下,线段OP与抛物线相交于点Q,若点Q恰好为OP的中点,此时对于在抛物线上且介于点C与抛物线顶点之间(含点C与顶点)的任意一点M(x0,y0)总能使不等式n≤![]() 及不等式2n﹣
及不等式2n﹣![]() 恒成立,求n的取值范围.
恒成立,求n的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y,的对应值如下表:
x | … | -2 | -1 | 0 | 1 | 2 | … |
y | … | 0 | -4 | -4 | 0 | 8 | … |
(1)根据上表填空:
①抛物线与x轴的交点坐标是_________和_________;
②抛物线经过点(-3,_________);
(2)试确定抛物线y=ax2+bx+c的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
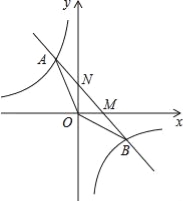
【题目】如图,已知一次函数y1=kx+b(k≠0)的图象与反比例函数![]() 的图象交于A、B两点,与坐标轴交于M、N两点.且点A的横坐标和点B的纵坐标都是﹣2.
的图象交于A、B两点,与坐标轴交于M、N两点.且点A的横坐标和点B的纵坐标都是﹣2.
(1)求一次函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出y1>y2时x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com