
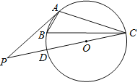
【题目】如图,已知![]() 、
、![]() 、
、![]() 分别是
分别是![]() 上的点,
上的点,![]() ,
,![]() 是直径
是直径![]() 的延长线上的一点,且
的延长线上的一点,且![]() .
.
(1)求证:![]() 与
与![]() 相切;
相切;
(2)如果![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)3.
【解析】
(1)利用圆周角定理以及等腰三角形的性质得出∠P=∠ACP=∠OCA=∠OAC=30°,∠PAC=120°,进而得出∠PAO=90°,即可得出答案;
(2)首先根据直角三角形中30°角所对的直角边等于斜边的一半求得半径,从而求得OA、OP,进而利用勾股定理得出AP的长.
(1)连接AO.
∵∠B=60°,∴∠AOC=120°.
∵AO=CO,AP=AC,∴∠P=∠ACP,∠OCA=∠OAC=30°,∴∠P=∠ACP=∠OCA=∠OAC=30°,∴∠PAC=120°,∴∠PAO=90°,∴AP是⊙O的切线;
(2)设⊙O的半径为R,则OA=OD=R,OP=![]() +R.
+R.
∵∠PAO=90°,∠P=30°,∴OP=2OA,即![]() +R=2R,解得:R=
+R=2R,解得:R=![]() ,∴OA=
,∴OA=![]() ,OP=2
,OP=2![]() ,∴PA=
,∴PA=![]() =
=![]() =3.
=3.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案科目:初中数学 来源: 题型:
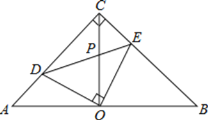
【题目】如图,在等腰直角![]() 中,
中,![]() ,
,![]() 是斜边
是斜边![]() 的中点,点
的中点,点![]() 、
、![]() 分别在直角边
分别在直角边![]() 、
、![]() 上,且
上,且![]() ,
,![]() 交
交![]() 于点
于点![]() .则下列结论:①图形中全等的三角形只有两对;②
.则下列结论:①图形中全等的三角形只有两对;②![]() 的面积等于四边形
的面积等于四边形![]() 面积的2倍;③
面积的2倍;③![]() ;④
;④![]() .其中正确的结论有_______________________________(填序号)
.其中正确的结论有_______________________________(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l的函数表达式为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径画圆,交直线l于点
为半径画圆,交直线l于点![]() ,交x轴正半轴于点
,交x轴正半轴于点![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径画圆,交直线l于点
为半径画圆,交直线l于点![]() ,交x轴正半轴于点
,交x轴正半轴于点![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径画圆,交直线l于点
为半径画圆,交直线l于点![]() ,交x轴正半轴于点
,交x轴正半轴于点![]() ;
;![]() 按此做法进行下去,其中
按此做法进行下去,其中![]() 的长为______.
的长为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
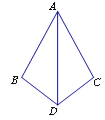
【题目】如图,在△ADB和△ADC中,下列条件:①BD=DC,AB=AC;②∠B=∠C,∠BAD=∠CAD;③∠B=∠C,BD=DC;④∠ADB=∠ADC,BD=DC.能得出△ADB≌△ADC的序号是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】过三角形一个顶点的直线,把原三角形分割成两个三角形,要求分得的两个三角形中至少有一个是等腰三角形.
(1)如果原三角形是顶点为108°的等腰三角形,这样的直线有________条.
(2)如果原三角形是等腰直角三角形,这样的直线有________条.
(3)如果原三角形是有一个锐角是30°的直角三角形,这样的直线有________条.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某草莓采摘园元旦至春节期间推出了甲、乙两种优惠方案.
甲种优惠方案:游客进园需要购买40元的门票(每个家庭购买一张门票),采摘的草莓均按定价的六折卖给采摘游客;
乙种优惠方案:游客进园不需购买门票,采摘的草莓按定价出售,但超过一定重量后,超过的部分打折卖给采摘的游客.
优惠期间,设某游客(或一个家庭)采摘草莓的重量为x(kg),选用甲种优惠方案采摘所需的总费用为y1(元),选用乙种优惠方案采摘所需的总费用为y2(元).已知1,y2与采摘重量x(kg)之间的函数关系如图所示.
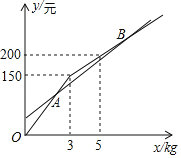
(1)分别求y1,y2与x之间的函数关系式;
(2)求点A的坐标,并解释坐标的实际意义;
(3)采摘重量x为多少时,游客选用甲种优惠方案采摘更合算.(直接写出答案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y,的对应值如下表:
x | … | -2 | -1 | 0 | 1 | 2 | … |
y | … | 0 | -4 | -4 | 0 | 8 | … |
(1)根据上表填空:
①抛物线与x轴的交点坐标是_________和_________;
②抛物线经过点(-3,_________);
(2)试确定抛物线y=ax2+bx+c的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com