
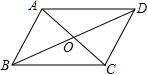
 如图,在?ABCD中,对角线AC、BD相交于点O,△AOB的周长是38cm,△BOC周长是30cm,△ABC的周长是44cm,△BCD的周长是52cm,求?ABCD的四条边长及两条对角线的长.
如图,在?ABCD中,对角线AC、BD相交于点O,△AOB的周长是38cm,△BOC周长是30cm,△ABC的周长是44cm,△BCD的周长是52cm,求?ABCD的四条边长及两条对角线的长. 分析 根据平行四边形的性质得出AO=CO,BO=DO,AB=DC,AD=BC,根据已知得出①AB+OA+OB=38cm,②BC+OB+OC=30cm,③DC+BC+BD=52cm,④AB+BC+AC=44cm,即可求出答案.
解答 解:∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO,AB=DC,AD=BC,
∵△AOB的周长是38cm,△BOC周长是30cm,△ABC的周长是44cm,△BCD的周长是52cm
∴①AB+OA+OB=38cm,②BC+OB+OC=30cm,③DC+BC+BD=52cm,④AB+BC+AC=44cm,
∴①-②得:AB-BC=8cm,
③+④-①-②得:AB+BC=28cm,
解得:AB=18cm,BC=10cm,
即AB=DC=18cmAD=BC=10cm,
代入④得:AC=44cm-18cm-10cm=16cm,
代入③得:BD=52cm-18cm-10cm=24cm,
即?ABCD的四条边长是10cm,18cm,10cm,18cm,两条对角线的长为16cm,24cm.
点评 本题考查了平行四边形的性质的应用,能正确运用性质进行推理是解此题的关键.


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
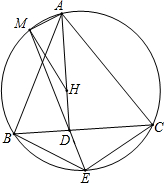 如图,△ABC的垂心为H,AD⊥BC于D,点E在△ABC的外接圆上,且满足$\frac{BE}{CE}=\frac{AB}{AC}$,直线ED交外接圆于点M.求证:∠AMH=90°.
如图,△ABC的垂心为H,AD⊥BC于D,点E在△ABC的外接圆上,且满足$\frac{BE}{CE}=\frac{AB}{AC}$,直线ED交外接圆于点M.求证:∠AMH=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
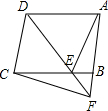 如图,过?ABCD的顶点D引一条直线交BC于E,交AB延长线于F.求证:
如图,过?ABCD的顶点D引一条直线交BC于E,交AB延长线于F.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com