
【题目】如图,在平面直角坐标系中,矩形OADB的顶点A,B的坐标分别为A(﹣6,0),B(0,4).过点C(﹣6,1)的双曲线y=![]() (k≠0)与矩形OADB的边BD交于点E.
(k≠0)与矩形OADB的边BD交于点E.
(1)填空:OA= ,k= ,点E的坐标为 ;
(2)当1≤t≤6时,经过点M(t﹣1,﹣![]() t2+5t﹣
t2+5t﹣![]() )与点N(﹣t﹣3,﹣
)与点N(﹣t﹣3,﹣![]() t2+3t﹣
t2+3t﹣![]() )的直线交y轴于点F,点P是过M,N两点的抛物线y=﹣
)的直线交y轴于点F,点P是过M,N两点的抛物线y=﹣![]() x2+bx+c的顶点.
x2+bx+c的顶点.
①当点P在双曲线y=![]() 上时,求证:直线MN与双曲线y=
上时,求证:直线MN与双曲线y=![]() 没有公共点;
没有公共点;
②当抛物线y=﹣![]() x2+bx+c与矩形OADB有且只有三个公共点,求t的值;
x2+bx+c与矩形OADB有且只有三个公共点,求t的值;
③当点F和点P随着t的变化同时向上运动时,求t的取值范围,并求在运动过程中直线MN在四边形OAEB中扫过的面积.

【答案】(1)6,﹣6,(﹣![]() ,4);(2)①证明见解析;②t=
,4);(2)①证明见解析;②t=![]() 或t=
或t=![]() ;③
;③![]() .
.
【解析】(1)根据题意将相关数据代入.
(2)①用t表示直线MN解析式,及b,c,得到P点坐标带入双曲线y=![]() 解析式,证明关于t的方程无解即可;
解析式,证明关于t的方程无解即可;
②根据抛物线开口和对称轴,分别讨论抛物线过点B和在BD上时的情况;
③由②中部分结果,用t表示F、P点的纵坐标,求出t的取值范围及直线MN在四边形OAEB中所过的面积.
解:(1)∵A点坐标为(﹣6,0)
∴OA=6
∵过点C(﹣6,1)的双曲线y=![]()
∴k=﹣6
y=4时,x=![]()
∴点E的坐标为(﹣![]() ,4)
,4)
故答案为:6,﹣6,(﹣![]() ,4)
,4)
(2)①设直线MN解析式为:y1=k1x+b1
由题意得: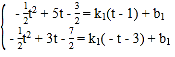
解得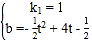 ,
,
∵抛物线y=﹣![]() 过点M、N,
过点M、N,
∴ ,
,
解得![]()
∴抛物线解析式为:y=﹣![]() x2﹣x+5t﹣2
x2﹣x+5t﹣2
∴顶点P坐标为(﹣1,5t﹣![]() )
)
∵P在双曲线y=﹣![]() 上
上
∴(5t﹣![]() )×(﹣1)=﹣6
)×(﹣1)=﹣6
∴t=![]()
此时直线MN解析式为:
联立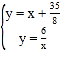
∴8x2+35x+49=0
∵△=352﹣4×8×48=1225﹣1536<0
∴直线MN与双曲线y=﹣![]() 没有公共点.
没有公共点.
②当抛物线过点B,此时抛物线y=﹣![]() x2+bx+c与矩形OADB有且只有三个公共点
x2+bx+c与矩形OADB有且只有三个公共点
∴4=5t﹣2,得t=![]()
当抛物线在线段DB上,此时抛物线与矩形OADB有且只有三个公共点
∴![]() ,得t=
,得t=![]()
∴t=![]() 或t=
或t=![]()
③∵点P的坐标为(﹣1,5t﹣![]() )
)
∴yP=5t﹣![]()
当1≤t≤6时,yP随t的增大而增大
此时,点P在直线x=﹣1上向上运动
∵点F的坐标为(0,﹣![]() )
)
∴yF=﹣![]()
∴当1≤t≤4时,随者yF随t的增大而增大
此时,随着t的增大,点F在y轴上向上运动
∴1≤t≤4
当t=1时,直线MN:y=x+3与x轴交于点G(﹣3,0),与y轴交于点H(0,3)
当t=4﹣![]() 时,直线MN过点A.
时,直线MN过点A.
当1≤t≤4时,直线MN在四边形AEBO中扫过的面积为
S=![]() .
.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
【题目】如图,BD是△ABC的角平分线,DE⊥AB,DF⊥BC垂足分别为E、F.

(1)求证:BE=BF;
(2)若△ABC的面积为70,AB=16,DE=5,则BC= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①![]() ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )

A. ①②③④ B. ①④ C. ②③④ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
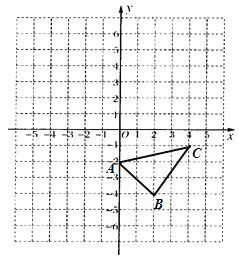
【题目】已知:如图,在平面直角坐标系中.
(1)作出△ABC关于![]() 轴对称的
轴对称的![]() ,并写出
,并写出![]() 三个顶点的坐标:
三个顶点的坐标: ![]() ( ),
( ),![]() ( ),
( ),![]() ( );
( );
(2)直接写出△ABC的面积为 ;
(3)在![]() 轴上画点P,使PA+PC最小.
轴上画点P,使PA+PC最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,△ABC是等腰三角形,AB=BC,点D为BC的中点.

(1)用圆规和没有刻度的直尺作图,并保留作图痕迹:
①过点B作AC的平行线BP;
②过点D作BP的垂线,分别交AC,BP,BQ于点E,F,G.
(2)在(1)所作的图中,连接BE,CF.求证:四边形BFCE是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
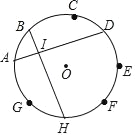
【题目】如图,点A,B,C,D,E,F,G,H为⊙O的八等分点,AD与BH的交点为I,若⊙O的半径为1,则HI的长等于( )
A. 2﹣![]() B. 2+
B. 2+ ![]() C. 2
C. 2![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
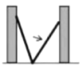
【题目】如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为( )
A.0.7米B.1.5米C.2.2米D.2.4米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合).在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)求证:△AEF是等腰直角三角形;
(2)如图2,将△CED绕点C逆时针旋转,当点E在线段BC上时,连接AE,求证:AF=![]() AE;
AE;
(3)如图3,将△CED绕点C继续逆时针旋转,当平行四边形ABFD为菱形,且△CED在△ABC的下方时,若AB=2![]() ,CE=2,求线段AE的长.
,CE=2,求线段AE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com