Question

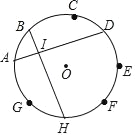
【题目】如图，点A，B，C，D，E，F，G，H为⊙O的八等分点，AD与BH的交点为I，若⊙O的半径为1，则HI的长等于（　　）

A. 2﹣ B. 2+ C. 2 D.

Answer 1

【答案】D

【解析】

连接AB、OH，作OM⊥AD于M，ON⊥BH于N，在IH上截取NK，使得ON=NK，连接OK．根据圆周角定理求出∠A=∠B=45°，∠H=22.5°，根据弧、弦、圆心角的关系及垂径定理可证明四边形OMIN是正方形，设OM=a，在Rt△ONH中，利用勾股定理列方程求出a的值，进而可求出HI的值.

如图，连接AB、OH，作OM⊥AD于M，ON⊥BH于N，在IH上截取NK，使得ON=NK，连接OK．

∵点A，B，C，D，E，F，G，H为⊙O的八等分点，

∴∠A=∠B==45°，∠H==22.5°，

∴∠AIB=90°，

∴∠MIN=∠OMI=∠ONI=90°，

∴四边形OMIN是矩形，

∵=，

∴AD=BH，

∴OM=ON，

∴四边形OMIN是正方形，设OM=a，

∵ON=NK，

∴∠OKN=45°，

∵∠OKN=∠H+∠KOH，

∴∠H=∠KOH=22.5°，

∴OK=KN=a，

在Rt△ONH中，a2+（a+a）2=1，

∴a=，

∴IH=（2+）a=．

故选：D．