
【题目】课间,小明拿着老师的等腰三角板玩,不小心掉到两墙之间,如图.
(1)求证:△ADC≌△CEB;
(2)从三角板的刻度可知AC=25cm,请你帮小明求出砌墙砖块的厚度a的大小(每块砖的厚度相等).

【答案】(1)证明见解析;(2)5cm.
【解析】
试题(1)根据题意可知AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,进而得到∠ADC=∠CEB=90°,再根据等角的余角相等可得∠BCE=∠DAC,从而得到结论;
(2)根据题意得:AD=4a,BE=3a,根据全等可得DC=BE=3a,由勾股定理可得(4a)2+(3a)2=252,再解即可.
试题解析:(1)根据题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC,
在△ADC和△CEB中,
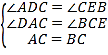 ,
,
∴△ADC≌△CEB(AAS);
(2)由题意得:AD=4a,BE=3a,
由(1)得:△ADC≌△CEB,
∴DC=BE=3a,
在Rt△ACD中:AD2+CD2=AC2,
∴(4a)2+(3a)2=252,
∵a>0,
解得a=5,
答:砌墙砖块的厚度a为5cm.
考点1.:全等三角形的应用2.勾股定理的应用.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
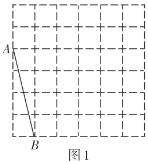
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.利用正方形网络可以画出长度为无理数的线段,如图1中![]() .请参考此方法按下列要求作图:
.请参考此方法按下列要求作图:
(1)在图1中以格点为顶点画一个面积为17的正方形![]() ,并标出字母;
,并标出字母;
(2)在图2中以格点为顶点画一个三角形![]() ,使
,使![]() ,
,![]() ,
,![]() ,并标出字母;
,并标出字母;
(3)猜想![]() 是何种特殊三角形.并说明理由.
是何种特殊三角形.并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有A、B两种型号的客车共11辆,它们的载客量(不含司机)、日租金、车辆数如下表所示,已知这11辆客车满载时可搭载乘客350人.
A型客车 | B型客车 | |
载客量(人/辆) | 40 | 25 |
日租金(元/辆) | 320 | 200 |
车辆数(辆) | a | b |
(1)求a、b的值;
(2)某校七年级师生周日集体参加社会实践,计划租用A、B两种型号的客车共6辆,且租车总费用不超过1700元.
①最多能租用A型客车多少辆?
②若七年级师生共195人,写出所有的租车方案,并确定最省钱的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=6,AB=4,点E、G、H、F分别在AB、BC、CD、AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连接PE、PF、PG、PH,则图中阴影面积(△PEF和△PGH的面积和)等于( )

A. 7 B. 8 C. 12 D. 14
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=60°,CE为△ABC的角平分线,AC边上的高BD与CE所在的直线交于点F,若∠ABD:∠ACF=2:3,则∠BEC的度数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
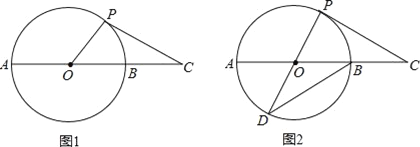
【题目】如图1,延长⊙O的直径AB至点C,使得BC=![]() AB,点P是⊙O上半部分的一个动点(点P不与A、B重合),连结OP,CP.
AB,点P是⊙O上半部分的一个动点(点P不与A、B重合),连结OP,CP.
(1)∠C的最大度数为 ;
(2)当⊙O的半径为3时,△OPC的面积有没有最大值?若有,说明原因并求出最大值;若没有,请说明理由;
(3)如图2,延长PO交⊙O于点D,连结DB,当CP=DB时,求证:CP是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知![]() 的边
的边![]() 平行于
平行于![]() 轴,
轴,![]() 点
点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在第四象限,点
在第四象限,点![]() 是
是![]() 边上的一个动点.
边上的一个动点.

(1)若点![]() 在边
在边![]() 上,
上,![]() 求点
求点![]() 的坐标;
的坐标;
(2)若点![]() 在边
在边![]() 或
或![]() 上,点
上,点![]() 是
是![]() 与
与![]() 轴的交点如图2,过点
轴的交点如图2,过点![]() 作
作![]() 轴的平行线
轴的平行线![]() 过点
过点![]() 作
作![]() 轴的平行线
轴的平行线![]() 它们相交于点
它们相交于点![]() ,将
,将![]() 沿直线
沿直线![]() 翻折,当点
翻折,当点![]() 的对应点落在坐标轴上时,求点
的对应点落在坐标轴上时,求点![]() 的坐标.(直接写出答案)
的坐标.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为美化校园,某学校将要购进A、B两个品种的树苗,已知一株A品种树苗比一株B品种树苗多20元,若买一株A品种树苗和2株B品种树苗共需110元.
(1)问A、B两种树苗每株分别是多少元?
(2)学校若花费不超过4000元购入A、B两种树苗,已知A品种树苗数量是B品种树苗数量的一半,问此次至多购买B品种树苗多少株?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com