
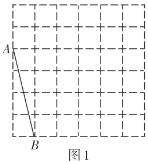
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.利用正方形网络可以画出长度为无理数的线段,如图1中![]() .请参考此方法按下列要求作图:
.请参考此方法按下列要求作图:
(1)在图1中以格点为顶点画一个面积为17的正方形![]() ,并标出字母;
,并标出字母;
(2)在图2中以格点为顶点画一个三角形![]() ,使
,使![]() ,
,![]() ,
,![]() ,并标出字母;
,并标出字母;
(3)猜想![]() 是何种特殊三角形.并说明理由.
是何种特殊三角形.并说明理由.

科目:初中数学 来源: 题型:
【题目】观察后填空:①(x﹣1)(x+1)=x2﹣1; ②(x﹣1)(x2+x+1)=x3﹣1; ③(x﹣1)(x3+x2+x+1)=x4﹣1.
(1)填空:(x﹣1)(x99+x98+x97+…+x+1)= .
(2)请利用上面的结论计算:
①(﹣2)50+(﹣2)49+(﹣2)48+…+(﹣2)+1; ②若x3+x2+x+1=0,求x2016的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点坐标分别为A(﹣6,0),B(4,0),C(0,8),把△ABC沿直线BC翻折,点A的对应点为D,抛物线y=ax2﹣10ax+c经过点C,顶点M在直线BC上.

(1)证明四边形ABCD是菱形,并求点D的坐标;
(2)求抛物线的对称轴和函数表达式;
(3)在抛物线上是否存在点P,使得△PBD与△PCD的面积相等?若存在,直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=x-6与x轴、y轴分别交于点A、B,点E从B点,出发以每秒1个单位的速度沿线段BO向O点移动(与B、O点不重合),过E作EF//AB,交x轴于F.将四边形ABEF沿EF折叠,得到四边形DCEF,设点E的运动时间为t秒.
(1)①直线y=x-6与坐标轴交点坐标是A(_____,______),B(______,_____);
②画出t=2时,四边形ABEF沿EF折叠后的图形(不写画法);
(2)若CD交y轴于H点,求证:四边形DHEF为平行四边形;并求t为何值时,四边形DHEF为菱形(计算结果不需化简);
(3)连接AD,BC四边形ABCD是什么图形,并求t为何值时,四边形ABCD的面积为36?

查看答案和解析>>
科目:初中数学 来源: 题型:
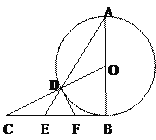
【题目】如图:已知AB是⊙O的直径,BC是⊙O的切线,OC与⊙O相交于点D,连结AD并延长,与BC相交于点E。
(1)若BC=![]() ,CD=1,求⊙O的半径;
,CD=1,求⊙O的半径;
(2)取BE的中点F,连结DF,求证:DF是⊙O的切线。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,对角线AC、BD相交于点O,设锐角∠AOB=α,将△DOC按逆时针方向旋转得到△D′OC′(0°<旋转角<90°)连接AC′、BD′,AC′与BD′相交于点M.

(1)、当四边形ABCD为矩形时,如图1.求证:△AOC′≌△BOD′.
(2)、当四边形ABCD为平行四边形时,设AC=kBD,如图2.
①猜想此时△AOC′与△BOD′有何关系,证明你的猜想;
②探究AC′与BD′的数量关系以及∠AMB与α的大小关系,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P、Q分别是正方形ABCD的边AB、BC上的点,且BP=BQ,过点B作PC的垂线,垂足为点H,连接HD、HQ. (14分)
(1)图中有________对相似三角形;
(2)若正方形ABCD的边长为1,P为AB的三等分点,求△BHQ的面积;
(3)求证:DH⊥HQ.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课间,小明拿着老师的等腰三角板玩,不小心掉到两墙之间,如图.
(1)求证:△ADC≌△CEB;
(2)从三角板的刻度可知AC=25cm,请你帮小明求出砌墙砖块的厚度a的大小(每块砖的厚度相等).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com