
【题目】直线y=x-6与x轴、y轴分别交于点A、B,点E从B点,出发以每秒1个单位的速度沿线段BO向O点移动(与B、O点不重合),过E作EF//AB,交x轴于F.将四边形ABEF沿EF折叠,得到四边形DCEF,设点E的运动时间为t秒.
(1)①直线y=x-6与坐标轴交点坐标是A(_____,______),B(______,_____);
②画出t=2时,四边形ABEF沿EF折叠后的图形(不写画法);
(2)若CD交y轴于H点,求证:四边形DHEF为平行四边形;并求t为何值时,四边形DHEF为菱形(计算结果不需化简);
(3)连接AD,BC四边形ABCD是什么图形,并求t为何值时,四边形ABCD的面积为36?

【答案】(1)①6,0,0,-6;②见详解;(2)证明见详解,当![]() 时,四边形DHEF为菱形;(3)四边形ABCD是矩形,当
时,四边形DHEF为菱形;(3)四边形ABCD是矩形,当![]() 时,四边形ABCD的面积为36.
时,四边形ABCD的面积为36.
【解析】
(1)①令![]() 求出x的值即可得到A的坐标,令
求出x的值即可得到A的坐标,令![]() 求出y的值即可得到B的坐标;
求出y的值即可得到B的坐标;
②先求出t=2时E,F的坐标,然后找到A,B关于EF的对称点,即可得到折叠后的图形;
(2)先利用对称的性质得出![]() ,然后利用平行线的性质和角度之间的关系得出
,然后利用平行线的性质和角度之间的关系得出![]() ,由此可证明四边形DHEF为平行四边形,要使四边形DHEF为菱形,只要
,由此可证明四边形DHEF为平行四边形,要使四边形DHEF为菱形,只要![]() ,利用
,利用![]() ,然后表示出EF,建立一个关于t的方程进而求解即可;
,然后表示出EF,建立一个关于t的方程进而求解即可;
(3)AB和CD关于EF对称,根据对称的性质可知四边形ABCD为平行四边形,由(2)知![]() ,即可判断四边形ABCD的形状,由
,即可判断四边形ABCD的形状,由![]() ,可知
,可知![]() ,建立关于四边形ABCD面积的方程解出t的值即可.
,建立关于四边形ABCD面积的方程解出t的值即可.
(1)①令![]() ,则
,则![]() ,解得
,解得![]() ,
,
∴![]() ;
;
令![]() , 则
, 则![]() ,
,
∴![]() ;
;
②当t=2时,![]() ,图形如下:
,图形如下:
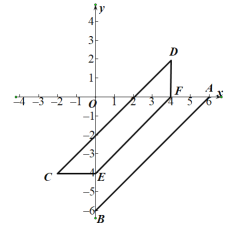
(2)如图,

∵四边形DCEF与四边形ABEF关于直线EF对称,![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
即![]() 轴,
轴,
![]() ,
,
∴四边形DHEF为平行四边形.
要使四边形DHEF为菱形,只需![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
又![]() ,
,
![]() ,
,
![]() ,
,
解得![]() ,
,
∴当![]() 时,四边形DHEF为菱形;
时,四边形DHEF为菱形;
(3)连接AD,BC,
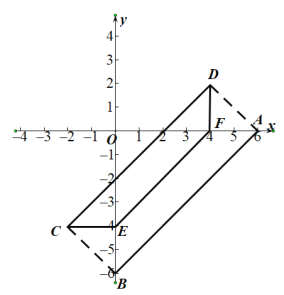
∵AB和CD关于EF对称,
∴![]() ,
,
∴四边形ABCD为平行四边形.
由(2)知![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
∴四边形ABCD为矩形.
∵![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
∴四边形ABCD的面积为![]() ,
,
解得![]() ,
,
∴当![]() 时,四边形ABCD的面积为36.
时,四边形ABCD的面积为36.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,边长为![]() 的等边
的等边![]() 的项点
的项点![]() 都在
都在![]() 轴上,顶点
轴上,顶点![]() 在第二象限内,
在第二象限内,![]() 经过平移或轴对称或旋转都可以得到
经过平移或轴对称或旋转都可以得到![]() .
.
(1)![]() 沿
沿![]() 轴向右平移得到
轴向右平移得到![]() ,则平移的距离是 个长度单位;
,则平移的距离是 个长度单位;![]() 与
与![]() 关于直线对称,则对称轴是 ,
关于直线对称,则对称轴是 ,![]() 绕原点
绕原点![]() 顺时针方向旋转得到
顺时针方向旋转得到![]() ,则旋转角度至少是 度;
,则旋转角度至少是 度;
(2)连接![]() ,交
,交![]() 于点
于点![]() ,求
,求![]() 的度数.
的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小东根据学习一次函数的经验,对函数y=|2x﹣1|的图象和性质进行了探究.下面是小东的探究过程,请补充完成:
(1)函数y=|2x﹣1|的自变量x的取值范围是 ;
(2)已知:
①当x=![]() 时,y=|2x﹣1|=0;
时,y=|2x﹣1|=0;
②当x>![]() 时,y=|2x﹣1|=2x﹣1
时,y=|2x﹣1|=2x﹣1
③当x<![]() 时,y=|2x﹣1|=1﹣2x;
时,y=|2x﹣1|=1﹣2x;
显然,②和③均为某个一次函数的一部分.
(3)由(2)的分析,取5个点可画出此函数的图象,请你帮小东确定下表中第5个点的坐标(m,n),其中m= ;n= ;:
x | … | ﹣2 | 0 |
| 1 | m | … |
y | … | 5 | 1 | 0 | 1 | n | … |
(4)在平面直角坐标系xOy中,作出函数y=|2x﹣1|的图象;
(5)根据函数的图象,写出函数y=|2x﹣1|的一条性质.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往B城,乙车驶往A城,甲车在行驶过程中速度始终不变.甲车距B城高速公路入口处的距离y(千米)与行驶时间x(时)之间的关系如图.
(1)求y关于x的表达式;
(2)已知乙车以60千米/时的速度匀速行驶,设行驶过程中,两车相距的路程为s(千米).请直接写出s关于x的表达式;
(3)当乙车按(2)中的状态行驶与甲车相遇后,速度随即改为a(千米/时)并保持匀速行驶,结果比甲车晚40分钟到达终点,求乙车变化后的速度a.在下图中画出乙车离开B城高速公路入口处的距离y(千米)与行驶时间x(时)之间的函数图象.
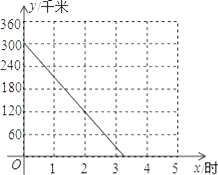
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小莹用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,BC长为10cm.当小莹折叠时,顶点D落在BC边上的点F处(折痕为AE).则此时EC=( )cm
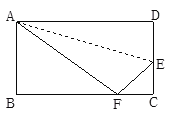
A.4B.![]() C.
C.![]() D.3
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
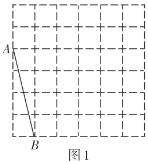
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.利用正方形网络可以画出长度为无理数的线段,如图1中![]() .请参考此方法按下列要求作图:
.请参考此方法按下列要求作图:
(1)在图1中以格点为顶点画一个面积为17的正方形![]() ,并标出字母;
,并标出字母;
(2)在图2中以格点为顶点画一个三角形![]() ,使
,使![]() ,
,![]() ,
,![]() ,并标出字母;
,并标出字母;
(3)猜想![]() 是何种特殊三角形.并说明理由.
是何种特殊三角形.并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为![]() ,C点的坐标为
,C点的坐标为![]() ,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着
,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着![]() 的路线移动
的路线移动![]() 即:沿着长方形移动一周
即:沿着长方形移动一周![]() .
.
![]() 写出点B的坐标
写出点B的坐标![]() ______
______![]()
![]() 当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
![]() 在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=6,AB=4,点E、G、H、F分别在AB、BC、CD、AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连接PE、PF、PG、PH,则图中阴影面积(△PEF和△PGH的面积和)等于( )

A. 7 B. 8 C. 12 D. 14
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com