
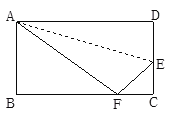
【题目】如图,小莹用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,BC长为10cm.当小莹折叠时,顶点D落在BC边上的点F处(折痕为AE).则此时EC=( )cm
A.4B.![]() C.
C.![]() D.3
D.3
【答案】D
【解析】
根据矩形的性质得AB=CD=8,BC=AD=10,∠B=∠C=90°,再根据折叠的性质得AF=AD=10,DE=EF,在Rt△ABF中,利用勾股定理计算出BF=6,则CF=BC﹣BF=4,设CE=x,则DE=EF=8﹣x,在Rt△CEF中利用勾股定理得到:42+x2=(8﹣x)2,然后解方程即可.
解:∵四边形ABCD为矩形,∴AB=CD=8,BC=AD=10,∠B=∠C=90°.
∵长方形纸片ABCD折纸,顶点D落在BC边上的点F处(折痕为AE),
∴AF=AD=10,DE=EF,
在Rt△ABF中,AB=8,AF=10,∴BF=![]()
∴CF=BC﹣BF=4.
设CE=x,则DE=EF=8﹣x,
在Rt△CEF中,∵CF2+CE2=EF2,
∴42+x2=(8﹣x)2,解得x=3
∴EC的长为3cm.
故选:D


科目:初中数学 来源: 题型:
【题目】(2015桂林)“全民阅读”深入人心,好读书,读好书,让人终身受益.为满足同学们的读书需求,学校图书馆准备到新华书店采购文学名著和动漫书两类图书.经了解,20本文学名著和40本动漫书共需1520元,20本文学名著比20本动漫书多440元(注:所采购的文学名著价格都一样,所采购的动漫书价格都一样).
(1)求每本文学名著和动漫书各多少元?
(2)若学校要求购买动漫书比文学名著多20本,动漫书和文学名著总数不低于72本,总费用不超过2000元,请求出所有符合条件的购书方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是把图1放入长方形内得到的,![]() ,AB=3,AC=4,点D,E,F,G,H,I都在长方形KLMJ的边上,则长方形KLMJ的面积为___.
,AB=3,AC=4,点D,E,F,G,H,I都在长方形KLMJ的边上,则长方形KLMJ的面积为___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=x-6与x轴、y轴分别交于点A、B,点E从B点,出发以每秒1个单位的速度沿线段BO向O点移动(与B、O点不重合),过E作EF//AB,交x轴于F.将四边形ABEF沿EF折叠,得到四边形DCEF,设点E的运动时间为t秒.
(1)①直线y=x-6与坐标轴交点坐标是A(_____,______),B(______,_____);
②画出t=2时,四边形ABEF沿EF折叠后的图形(不写画法);
(2)若CD交y轴于H点,求证:四边形DHEF为平行四边形;并求t为何值时,四边形DHEF为菱形(计算结果不需化简);
(3)连接AD,BC四边形ABCD是什么图形,并求t为何值时,四边形ABCD的面积为36?

查看答案和解析>>
科目:初中数学 来源: 题型:
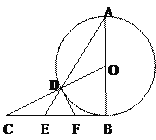
【题目】如图:已知AB是⊙O的直径,BC是⊙O的切线,OC与⊙O相交于点D,连结AD并延长,与BC相交于点E。
(1)若BC=![]() ,CD=1,求⊙O的半径;
,CD=1,求⊙O的半径;
(2)取BE的中点F,连结DF,求证:DF是⊙O的切线。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红同学要测量![]() ,
,![]() 两地的距离,但
两地的距离,但![]() ,
,![]() 之间有一水池,不能直接测量,于是她在
之间有一水池,不能直接测量,于是她在![]() ,
,![]() 同一水平面上选取了一点
同一水平面上选取了一点![]() ,点
,点![]() 可直接到达
可直接到达![]() ,
,![]() 两地.她测量得到
两地.她测量得到![]() 米,
米,![]() 米,
米,![]() .请你帮助小红同学求出
.请你帮助小红同学求出![]() ,
,![]() 两点之间的距离.
两点之间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产![]() 两种设备,已知每台
两种设备,已知每台![]() 种设备的成本是
种设备的成本是![]() 种设备的1.5倍,公司若投入6万元生产
种设备的1.5倍,公司若投入6万元生产![]() 种设备,投人15万元生产
种设备,投人15万元生产![]() 种设备,则可生产两种设备共40台.请解答下列问题:
种设备,则可生产两种设备共40台.请解答下列问题:
(1)![]() 两种设备每台的成本分别是多少万元?
两种设备每台的成本分别是多少万元?
(2)若![]() 两种设备每台的售价分别是5000元、9000元,公司决定生产两种设备共50台,且其中
两种设备每台的售价分别是5000元、9000元,公司决定生产两种设备共50台,且其中![]() 种设备至少生产10台,计划销售后获利不低于12万元,请问采用哪种生产方案公司所获利润最大?并求出最大利润.
种设备至少生产10台,计划销售后获利不低于12万元,请问采用哪种生产方案公司所获利润最大?并求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com