
【题目】勾股定理是几何中的一个重要定理.在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是把图1放入长方形内得到的,![]() ,AB=3,AC=4,点D,E,F,G,H,I都在长方形KLMJ的边上,则长方形KLMJ的面积为___.
,AB=3,AC=4,点D,E,F,G,H,I都在长方形KLMJ的边上,则长方形KLMJ的面积为___.

【答案】110
【解析】
延长AB交KF于点O,延长AC交GM于点P,可得四边形AOLP是正方形,然后求出正方形的边长,再求出矩形KLMJ的长与宽,然后根据矩形的面积公式列式计算即可得解.
如图,延长AB交KF于点O,延长AC交GM于点P,则四边形OALP是矩形.
∵∠CBF=90°,
∴∠ABC+∠OBF=90°,
又∵直角△ABC中,∠ABC+∠ACB=90°,
∴∠OBF=∠ACB,
在△OBF和△ACB中,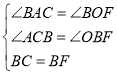 ,
,
∴△OBF≌△ACB(AAS),
∴AC=OB,
同理:△ACB≌△PGC,
∴PC=AB,
∴OA=AP,
所以,矩形AOLP是正方形,
边长AO=AB+AC=3+4=7,
所以,KL=3+7=10,LM=4+7=11,
因此,矩形KLMJ的面积为10×11=110.


科目:初中数学 来源: 题型:
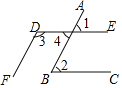
【题目】如图,∠1=60°,∠2=60°,∠3=120°.
试说明DE∥BC,DF∥AB,根据图形,完成下列推理:
∵∠1=60°,∠2=60°(已知)
∴∠1=∠2(等量代换)
∴ ∥ ( )
∵AB,DE相交,
∴∠4=∠1=60°
∵∠3=120°
∴∠3+∠4=180°
∴ ∥ ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,点
两点,点![]() 是
是![]() 轴上一动点,要使点
轴上一动点,要使点![]() 关于直线
关于直线![]() 的对称点刚好落在
的对称点刚好落在![]() 轴上,则此时点
轴上,则此时点![]() 的坐标是( )
的坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD⊥BC,EG⊥BC,垂足分别为D、G、AD平分∠BAC,求证:∠E=∠4.
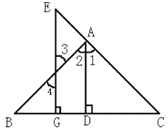
证明:∵AD⊥BC,EG⊥BC(已知)
∴AD∥EG( )
∴∠2=∠3( )
∠1= (两直线平行,同位角相等)
∵AD平分∠BAC(已知)
∴∠1=∠2( )
∴∠E=∠3( )
∵∠3=∠4( )
∴∠E=∠4(等量代换)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小东根据学习一次函数的经验,对函数y=|2x﹣1|的图象和性质进行了探究.下面是小东的探究过程,请补充完成:
(1)函数y=|2x﹣1|的自变量x的取值范围是 ;
(2)已知:
①当x=![]() 时,y=|2x﹣1|=0;
时,y=|2x﹣1|=0;
②当x>![]() 时,y=|2x﹣1|=2x﹣1
时,y=|2x﹣1|=2x﹣1
③当x<![]() 时,y=|2x﹣1|=1﹣2x;
时,y=|2x﹣1|=1﹣2x;
显然,②和③均为某个一次函数的一部分.
(3)由(2)的分析,取5个点可画出此函数的图象,请你帮小东确定下表中第5个点的坐标(m,n),其中m= ;n= ;:
x | … | ﹣2 | 0 |
| 1 | m | … |
y | … | 5 | 1 | 0 | 1 | n | … |
(4)在平面直角坐标系xOy中,作出函数y=|2x﹣1|的图象;
(5)根据函数的图象,写出函数y=|2x﹣1|的一条性质.

查看答案和解析>>
科目:初中数学 来源: 题型:
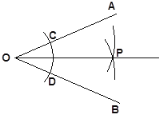
【题目】同学们已经学过用尺规作一条线段等于已知线段、作一个角等于已知角.请同学们看下面一个尺规作图的例子:
①以O为圆心,任意长为半径作弧线交∠AOB的两边OA、OB分别于C、D两点;
②以C为圆心,大于![]() CD的长为半径作弧线,再以D为圆心,同样的长为半径作弧线,两弧线交于P点;
CD的长为半径作弧线,再以D为圆心,同样的长为半径作弧线,两弧线交于P点;
③以O为端点作射线OP.
则OP就是∠AOB的平分线
你知道OP为什么是∠AOB的角平分线吗?请用你所学的知识解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
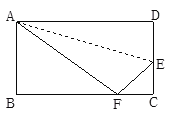
【题目】如图,小莹用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,BC长为10cm.当小莹折叠时,顶点D落在BC边上的点F处(折痕为AE).则此时EC=( )cm
A.4B.![]() C.
C.![]() D.3
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,A(a,0)是x轴正半轴上一点,C是第四象限一点,CB⊥y轴,交y轴负半轴于B(0,b),且(a-3)2+|b+4|=0,S四边形AOBC=16.
(1)求C点坐标;
(2)如图2,设D为线段OB上一动点,当AD⊥AC时,∠ODA的角平分线与∠CAE的角平分线的反向延长线交于点P,求∠APD的度数.
(3)如图3,当D点在线段OB上运动时,作DM⊥AD交BC于M点,∠BMD、∠DAO的平分线交于N点,则D点在运动过程中,∠N的大小是否变化?若不变,求出其值,若变化,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com