
ЁОЬтФПЁПЭЌбЇУЧвбОбЇЙ§гУГпЙцзївЛЬѕЯпЖЮЕШгквбжЊЯпЖЮЁЂзївЛИіНЧЕШгквбжЊНЧ.ЧыЭЌбЇУЧПДЯТУцвЛИіГпЙцзїЭМЕФР§згЃК
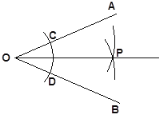
ЂйвдOЮЊдВаФЃЌШЮвтГЄЮЊАыОЖзїЛЁЯпНЛЁЯAOBЕФСНБпOAЁЂOBЗжБ№гкCЁЂDСНЕуЃЛ
ЂквдCЮЊдВаФЃЌДѓгк![]() CDЕФГЄЮЊАыОЖзїЛЁЯпЃЌдйвдDЮЊдВаФЃЌЭЌбљЕФГЄЮЊАыОЖзїЛЁЯпЃЌСНЛЁЯпНЛгкPЕуЃЛ
CDЕФГЄЮЊАыОЖзїЛЁЯпЃЌдйвдDЮЊдВаФЃЌЭЌбљЕФГЄЮЊАыОЖзїЛЁЯпЃЌСНЛЁЯпНЛгкPЕуЃЛ
ЂлвдOЮЊЖЫЕузїЩфЯпOP.
дђOPОЭЪЧЁЯAOBЕФЦНЗжЯп
ФужЊЕРOPЮЊЪВУДЪЧЁЯAOBЕФНЧЦНЗжЯпТ№ЃПЧыгУФуЫљбЇЕФжЊЪЖНтЪЭ.
 ЛЦИдЬьЬьСЗПкЫуЬтПЈЯЕСаД№АИ
ЛЦИдЬьЬьСЗПкЫуЬтПЈЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМБэЪОвЛСОЦћГЕдкааЪЛЭОжаЕФЫйЖШvЃЈЧЇУз/ЪБЃЉЫцЪБМфtЃЈЗжЃЉЕФБфЛЏЪОвтЭМЃК
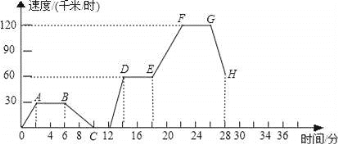
ЃЈ1ЃЉДгЕуAЕНЕуBЁЂЕуEЕНЕуFЁЂЕуGЕНЕуHЗжБ№БэУїЦћГЕдкЪВУДзДЬЌЃП
ЃЈ2ЃЉЗжЖЮУшЪіЦћГЕдкЕк0ЗжжжЕНЕк28ЗжжгЕФааЪЛЧщПіЃЛ
ЃЈ3ЃЉЦћГЕдкЕуAЕФЫйЖШЪЧЖрЩйЃПдкЕуCФиЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвУЧАбСНЬѕжаЯпЛЅЯрДЙжБЕФШ§НЧаЮГЦЮЊЁАжаДЙШ§НЧаЮЁБЃЌР§ШчЭМ1ЃЌЭМ2ЃЌЭМ3жаЃЌAFЃЌBEЪЧЁїABCЕФжаЯпЃЌAFЁЭBEЃЌДЙзуЮЊPЃЌЯёЁїABCетбљЕФШ§НЧаЮОљЮЊЁАжаДЙШ§НЧаЮЁБЃЌЩшBC=aЃЌACЉbЃЌAB=cЃЎ
ЁОЬиР§ЬНЫїЁП
ЃЈ1ЃЉШчЭМ1ЃЌЕБЁЯABE=45ЁуЃЌc=2![]() ЪБЃЌa=ЁЁ ЁЁЃЌb=ЁЁ ЁЁЃЛШчЭМ2ЃЌЕБЁЯABE=30ЁуЃЌc=4ЪБЃЌa=ЁЁ ЁЁЃЌb=ЁЁ ЁЁЃЛ
ЪБЃЌa=ЁЁ ЁЁЃЌb=ЁЁ ЁЁЃЛШчЭМ2ЃЌЕБЁЯABE=30ЁуЃЌc=4ЪБЃЌa=ЁЁ ЁЁЃЌb=ЁЁ ЁЁЃЛ
ЁОЙщФЩжЄУїЁП
ЃЈ2ЃЉЧыФуЙлВьЃЈ1ЃЉжаЕФМЦЫуНсЙћЃЌВТЯыa2ЃЌb2ЃЌc2Ш§епжЎМфЕФЙиЯЕЃЌгУЕШЪНБэЪОГіРДЃЌЧыРћгУЭМ3жЄУїФуЗЂЯжЕФЙиЯЕЪНЃЛ
ЁОЭиеЙгІгУЁП
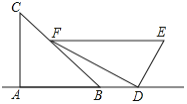
ЃЈ3ЃЉШчЭМ4ЃЌдкABCDжаЃЌЕуEЃЌFЃЌGЗжБ№ЪЧADЃЌBCЃЌCDЕФжаЕуЃЌBEЁЭEGЃЌAD=2![]() ЃЌAB=3ЃЎЧѓAFЕФГЄЃЎ
ЃЌAB=3ЃЎЧѓAFЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП![]() СНЕиЯрОр
СНЕиЯрОр![]() ЃЌМзЁЂввЖўШЫЗжБ№ЦяздааГЕКЭФІЭаГЕбиЯрЭЌТЗЯпдШЫйааЪЛЃЌгЩ
ЃЌМзЁЂввЖўШЫЗжБ№ЦяздааГЕКЭФІЭаГЕбиЯрЭЌТЗЯпдШЫйааЪЛЃЌгЩ![]() ЕиЕНДя
ЕиЕНДя![]() ЕиЃЎЫћУЧааЪЛЕФТЗГЬ
ЕиЃЎЫћУЧааЪЛЕФТЗГЬ![]() гыМзГіЗЂКѓЕФЪБМф
гыМзГіЗЂКѓЕФЪБМф![]() жЎМфЕФКЏЪ§ЭМЯёШчЭМЫљЪОЃЎ
жЎМфЕФКЏЪ§ЭМЯёШчЭМЫљЪОЃЎ
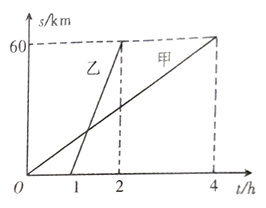
ЃЈ1ЃЉввБШМзЭэГіЗЂМИаЁЪБЃПввБШМздчЕНМИаЁЪБЃП
ЃЈ2ЃЉЗжБ№аДГіМзЁЂввааЪЛЕФТЗГЬ![]() гыМзГіЗЂКѓЕФЪБМф
гыМзГіЗЂКѓЕФЪБМф![]() ЕФКЏЪ§ЙиЯЕЪН(ВЛаДздБфСПЕФШЁжЕЗЖЮЇ)ЃЎ
ЕФКЏЪ§ЙиЯЕЪН(ВЛаДздБфСПЕФШЁжЕЗЖЮЇ)ЃЎ
ЃЈ3ЃЉввдкМзГіЗЂКѓМИаЁЪБзЗЩЯМзЃПзЗЩЯМзЕФЕиЕуРы![]() ЕигаЖрдЖЃП
ЕигаЖрдЖЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙДЙЩЖЈРэЪЧМИКЮжаЕФвЛИіживЊЖЈРэЃЎдкЮвЙњЙХЫуЪщЁЖжмїТЫуОЁЗжаОЭгаЁАШєЙДШ§ЃЌЙЩЫФЃЌдђЯвЮхЁБЕФМЧдиЃЎШчЭМ1ЪЧгЩБпГЄЯрЕШЕФаЁе§ЗНаЮКЭжБНЧШ§НЧаЮЙЙГЩЕФЃЌПЩвдгУЦфУцЛ§ЙиЯЕбщжЄЙДЙЩЖЈРэЃЎЭМ2ЪЧАбЭМ1ЗХШыГЄЗНаЮФкЕУЕНЕФЃЌ![]() ЃЌAB=3ЃЌAC=4ЃЌЕуDЃЌEЃЌFЃЌGЃЌHЃЌIЖМдкГЄЗНаЮKLMJЕФБпЩЯЃЌдђГЄЗНаЮKLMJЕФУцЛ§ЮЊ___ЃЎ
ЃЌAB=3ЃЌAC=4ЃЌЕуDЃЌEЃЌFЃЌGЃЌHЃЌIЖМдкГЄЗНаЮKLMJЕФБпЩЯЃЌдђГЄЗНаЮKLMJЕФУцЛ§ЮЊ___ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌEFЁЮADЃЌЁЯ1ЃНЁЯ2ЃЌЁЯBACЃН70ЁуЃЎНЋЧѓЁЯAGDЕФЙ§ГЬЬюаДЭъећЃЎ

ЁпEFЁЮADЃЌЃЈЁЁ ЁЁЃЉ
ЁрЁЯ2ЃНЁЁ ЁЁЃЎЃЈСНжБЯпЦНааЃЌЭЌЮЛНЧЯрЕШЃЉ
гжЁпЁЯ1ЃНЁЯ2ЃЌЃЈЁЁ ЁЁЃЉ
ЁрЁЯ1ЃНЁЯ3ЃЎЃЈЁЁ ЁЁЃЉ
ЁрABЁЮDGЃЎЃЈЁЁ ЁЁЃЉ
ЁрЁЯBAC+ЁЁ ЁЁЃН180ЁуЃЈЁЁ ЁЁЃЉ
гжЁпЁЯBACЃН70ЁуЃЌЃЈЁЁ ЁЁЃЉ
ЁрЁЯAGDЃНЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩЦгкЫМПМЕФаЁіЮЭЌбЇЃЌдквЛДЮЪ§бЇЛюЖЏжаЃЌНЋвЛИБжБНЧШ§НЧАхШчЭМЗХжУЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() дкЭЌвЛжБЯпЩЯЃЌЧв
дкЭЌвЛжБЯпЩЯЃЌЧв![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌСПЕУ
ЃЌСПЕУ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
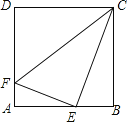
ЁОЬтФПЁПвбжЊе§ЗНаЮABCDЕФБпГЄЮЊ4ЃЌEЮЊABЕФжаЕуЃЌFЮЊADЩЯвЛЕуЃЌЧвAF=![]() ADЃЌЪдХаЖЯЁїEFCЕФаЮзДЃЎ
ADЃЌЪдХаЖЯЁїEFCЕФаЮзДЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЖЏЕуPдкЦНУцжБНЧзјБъЯЕжаАДЭМжаМ§ЭЗЫљЪОЗНЯђдЫЖЏЃЌЕк1ДЮДгдЕудЫЖЏЕНЕуЃЈ1ЃЌ1ЃЉЃЌЕк2ДЮНгзХдЫЖЏЕНЕуЃЈ2ЃЌ0ЃЉЃЌЕк3ДЮНгзХдЫЖЏЕНЕуЃЈ3ЃЌ2ЃЉЃЌЁЁЃЌАДетбљЕФдЫЖЏЙцТЩЃЌОЙ§Ек2019ДЮдЫЖЏКѓЃЌЖЏЕуPЕФзјБъЪЧЃЈЁЁЁЁЃЉ

A. ЃЈ2018ЃЌ1ЃЉB. ЃЈ2018,0ЃЉC. ЃЈ2019,2ЃЉ D. ЃЈ2019,1ЃЉ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com