
【题目】如图,在直角坐标系中,边长为![]() 的等边
的等边![]() 的项点
的项点![]() 都在
都在![]() 轴上,顶点
轴上,顶点![]() 在第二象限内,
在第二象限内,![]() 经过平移或轴对称或旋转都可以得到
经过平移或轴对称或旋转都可以得到![]() .
.
(1)![]() 沿
沿![]() 轴向右平移得到
轴向右平移得到![]() ,则平移的距离是 个长度单位;
,则平移的距离是 个长度单位;![]() 与
与![]() 关于直线对称,则对称轴是 ,
关于直线对称,则对称轴是 ,![]() 绕原点
绕原点![]() 顺时针方向旋转得到
顺时针方向旋转得到![]() ,则旋转角度至少是 度;
,则旋转角度至少是 度;
(2)连接![]() ,交
,交![]() 于点
于点![]() ,求
,求![]() 的度数.
的度数.

【答案】(1)2,![]() 轴,
轴,![]() ;(2)90°
;(2)90°
【解析】
(1)直接利用平移、对称,旋转的定义求解即可;
(2)根据△AOC和△DOB是能够重合的等边三角形得到AO=DO,然后利用∠AOC=∠COD=60°得到OE⊥AD,从而得到∠AEO=90°.
解:(1)边长为![]() 的等边△AOC沿数轴向右平移得到△OBD,则平移的距离是2个单位长度;△AOC与△BOD关于直线对称,则对称轴是y轴;△AOC绕原点O顺时针旋转得到△DOB,则旋转角度至少是120°度,
的等边△AOC沿数轴向右平移得到△OBD,则平移的距离是2个单位长度;△AOC与△BOD关于直线对称,则对称轴是y轴;△AOC绕原点O顺时针旋转得到△DOB,则旋转角度至少是120°度,
故答案为:2;y轴;120;
(2)∵△AOC和△DOB是能够重合的等边三角形,
∴AO=DO,∠AOC=∠COD=60°,
∴OE⊥AD,
∴∠AEO=90°.


科目:初中数学 来源: 题型:
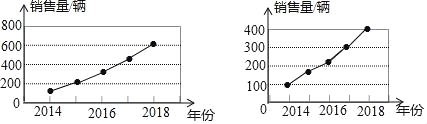
【题目】甲,乙两家汽车销售公司根据近几年的销售量分别制作了如图所示的统计图,从2014~2018年,这两家公司中销售量增长较快的是_____公司(填“甲”或“乙”).
查看答案和解析>>
科目:初中数学 来源: 题型:
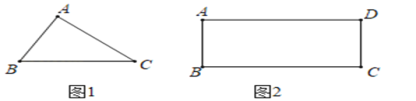
【题目】(1)如图1,已知△ABC,试确定一点D,使得以A,B,C,D为顶点的四边形为平行四边形,请画出这个平行四边形;
(2)如图2,在矩形ABCD中,AB=4,BC=10,若要在该矩形中作出一个面积最大的△BPC,且使∠BPC=90°,求满足条件的点P到点A的距离;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BD是角平分线,且∠ACB=60°,∠ADB=97°,
(1)求∠A
(2) 在图中画出△ABC边AB上的高CE.并求出∠ACE的度数.
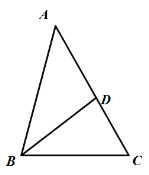
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解我县中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图所示.请根据图表信息解答下列问题.
组别 | 分数段(分) | 频数 | 百分率(%) |
A组 | 60≤x<70 | 30 | 10 |
B组 | 70≤x<80 | 90 | n |
C组 | 80≤x<90 | m | 40 |
D组 | 90≤x<100 | 60 | 20 |
(1)样本容量a= ,表中m= ,n= ;
(2)补全频数分布直方图;
(3)若成绩在80分以上(包括80分)为“优”等,请你估计我县参加“科普知识”竞赛的1.5万名学生中成绩是“优”等的约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2015桂林)“全民阅读”深入人心,好读书,读好书,让人终身受益.为满足同学们的读书需求,学校图书馆准备到新华书店采购文学名著和动漫书两类图书.经了解,20本文学名著和40本动漫书共需1520元,20本文学名著比20本动漫书多440元(注:所采购的文学名著价格都一样,所采购的动漫书价格都一样).
(1)求每本文学名著和动漫书各多少元?
(2)若学校要求购买动漫书比文学名著多20本,动漫书和文学名著总数不低于72本,总费用不超过2000元,请求出所有符合条件的购书方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察后填空:①(x﹣1)(x+1)=x2﹣1; ②(x﹣1)(x2+x+1)=x3﹣1; ③(x﹣1)(x3+x2+x+1)=x4﹣1.
(1)填空:(x﹣1)(x99+x98+x97+…+x+1)= .
(2)请利用上面的结论计算:
①(﹣2)50+(﹣2)49+(﹣2)48+…+(﹣2)+1; ②若x3+x2+x+1=0,求x2016的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,对角线AC,BD交于点O,折叠正方形ABCD,使AB边落在AC上,点B落在点H处,折痕AE分别交BC于点E,交BO于点F,连结FH,则下列结论(1)AD=DF;(2)![]() =
=![]() ;(3)
;(3)![]() =
=![]() ﹣1;(4)四边形BEHF为菱形.正确的有几个( )
﹣1;(4)四边形BEHF为菱形.正确的有几个( )
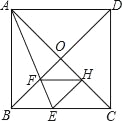
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=x-6与x轴、y轴分别交于点A、B,点E从B点,出发以每秒1个单位的速度沿线段BO向O点移动(与B、O点不重合),过E作EF//AB,交x轴于F.将四边形ABEF沿EF折叠,得到四边形DCEF,设点E的运动时间为t秒.
(1)①直线y=x-6与坐标轴交点坐标是A(_____,______),B(______,_____);
②画出t=2时,四边形ABEF沿EF折叠后的图形(不写画法);
(2)若CD交y轴于H点,求证:四边形DHEF为平行四边形;并求t为何值时,四边形DHEF为菱形(计算结果不需化简);
(3)连接AD,BC四边形ABCD是什么图形,并求t为何值时,四边形ABCD的面积为36?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com