
【题目】在四边形ABCD中,对角线AC、BD相交于点O,设锐角∠AOB=α,将△DOC按逆时针方向旋转得到△D′OC′(0°<旋转角<90°)连接AC′、BD′,AC′与BD′相交于点M.

(1)、当四边形ABCD为矩形时,如图1.求证:△AOC′≌△BOD′.
(2)、当四边形ABCD为平行四边形时,设AC=kBD,如图2.
①猜想此时△AOC′与△BOD′有何关系,证明你的猜想;
②探究AC′与BD′的数量关系以及∠AMB与α的大小关系,并给予证明.
【答案】(1)见解析;(2)①、△BOD′∽△AOC′;(2)AC′=kBD′,∠AMB=α.
【解析】试题分析:(1)证明:在矩形ABCD中,AC=BD,OA=OC=![]() AC,OB=OD=
AC,OB=OD=![]() BD,∴OA=OC=OB=OD,又∵OD=OD′,OC=OC′,∴OB=OD′=OA=OC′,∵∠D′OD=∠C′OC,∴180°﹣∠D′OD=180°﹣∠C′OC,∴∠BOD′=∠AOC′,∴在△BOD′和△AOC′中,
BD,∴OA=OC=OB=OD,又∵OD=OD′,OC=OC′,∴OB=OD′=OA=OC′,∵∠D′OD=∠C′OC,∴180°﹣∠D′OD=180°﹣∠C′OC,∴∠BOD′=∠AOC′,∴在△BOD′和△AOC′中,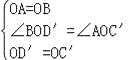 ,∴△BOD′≌△AOC′;
,∴△BOD′≌△AOC′;
(2)解:①△AOC′∽△BOD′;理由如下:∵在平行四边形ABCD中,OB=OD,OA=OC,又∵OD=OD′,OC=OC′,∴OC′=OA,OD′=OB,∵∠D′OD=∠C′OC,∴180°﹣∠D′OD=180°﹣∠C′OC,∴∠BOD′=∠AOC′,∴△BOD′∽△AOC′,∴BD′:AC′=OB:OA=BD:AC,∵AC=kBD,∴AC′=kBD′,∴△BOD′∽△AOC′;
②AC′=kBD′,∠AMB=α;设BD′与OA相交于点N,∴∠BNO=∠ANM,∴180°﹣∠OAC′﹣∠ANM=180°﹣∠OBD′﹣∠BNO,即∠AMB=∠AOB=α,综上所述,AC′=kBD′,∠AMB=α.


 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 的函数表达式为
的函数表达式为![]() ,与
,与![]() 轴交点为
轴交点为![]() ,与
,与![]() 轴交点为
轴交点为![]() .
.
(1)求![]() 两点的坐标;
两点的坐标;
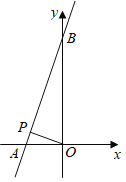
(2)若点![]() 为线段
为线段![]() 上的一个动点,
上的一个动点,![]() 为坐标原点,是否存在点
为坐标原点,是否存在点![]() ,使
,使![]() 的值最小?若存在,求出
的值最小?若存在,求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
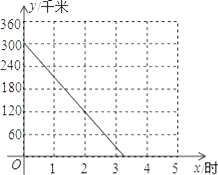
【题目】A、B两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往B城,乙车驶往A城,甲车在行驶过程中速度始终不变.甲车距B城高速公路入口处的距离y(千米)与行驶时间x(时)之间的关系如图.
(1)求y关于x的表达式;
(2)已知乙车以60千米/时的速度匀速行驶,设行驶过程中,两车相距的路程为s(千米).请直接写出s关于x的表达式;
(3)当乙车按(2)中的状态行驶与甲车相遇后,速度随即改为a(千米/时)并保持匀速行驶,结果比甲车晚40分钟到达终点,求乙车变化后的速度a.在下图中画出乙车离开B城高速公路入口处的距离y(千米)与行驶时间x(时)之间的函数图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
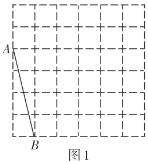
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.利用正方形网络可以画出长度为无理数的线段,如图1中![]() .请参考此方法按下列要求作图:
.请参考此方法按下列要求作图:
(1)在图1中以格点为顶点画一个面积为17的正方形![]() ,并标出字母;
,并标出字母;
(2)在图2中以格点为顶点画一个三角形![]() ,使
,使![]() ,
,![]() ,
,![]() ,并标出字母;
,并标出字母;
(3)猜想![]() 是何种特殊三角形.并说明理由.
是何种特殊三角形.并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题解决:
如图1,已知正方形![]() ,
,![]() ,把含
,把含![]() (
(![]() )的直角三角板的一个锐角顶点和点
)的直角三角板的一个锐角顶点和点![]() 重合,三角板和正方形的
重合,三角板和正方形的![]() ,
,![]() 两边分别相交于
两边分别相交于![]() ,
,![]() 两点.
两点.
(1)当![]() 时,求
时,求![]() 的长;
的长;
探究发现:
(2)在图1的基础上,试探究![]() ,
,![]() ,
,![]() 有怎样的数量关系,请写出猜想,并给予证明.
有怎样的数量关系,请写出猜想,并给予证明.
类比延伸:
(3)如图2,若三角板和正方形![]() ,
,![]() 两边的延长线分别相交于
两边的延长线分别相交于![]() ,
,![]() 两点,请直接写出
两点,请直接写出![]() ,
,![]() ,
,![]() 存在的数量关系.
存在的数量关系.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为![]() ,C点的坐标为
,C点的坐标为![]() ,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着
,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着![]() 的路线移动
的路线移动![]() 即:沿着长方形移动一周
即:沿着长方形移动一周![]() .
.
![]() 写出点B的坐标
写出点B的坐标![]() ______
______![]()
![]() 当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
![]() 在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
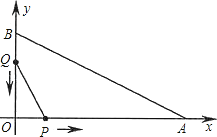
【题目】如图,在平面直角坐标系中,已知OA=12厘米,OB=6厘米.点P从点O开始沿OA边向点A以1厘米/秒的速度移动;点Q从点B开始沿BO边向点O以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6),那么,当t为何值时,△POQ与△AOB相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有A、B两种型号的客车共11辆,它们的载客量(不含司机)、日租金、车辆数如下表所示,已知这11辆客车满载时可搭载乘客350人.
A型客车 | B型客车 | |
载客量(人/辆) | 40 | 25 |
日租金(元/辆) | 320 | 200 |
车辆数(辆) | a | b |
(1)求a、b的值;
(2)某校七年级师生周日集体参加社会实践,计划租用A、B两种型号的客车共6辆,且租车总费用不超过1700元.
①最多能租用A型客车多少辆?
②若七年级师生共195人,写出所有的租车方案,并确定最省钱的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
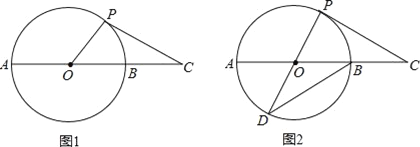
【题目】如图1,延长⊙O的直径AB至点C,使得BC=![]() AB,点P是⊙O上半部分的一个动点(点P不与A、B重合),连结OP,CP.
AB,点P是⊙O上半部分的一个动点(点P不与A、B重合),连结OP,CP.
(1)∠C的最大度数为 ;
(2)当⊙O的半径为3时,△OPC的面积有没有最大值?若有,说明原因并求出最大值;若没有,请说明理由;
(3)如图2,延长PO交⊙O于点D,连结DB,当CP=DB时,求证:CP是⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com