
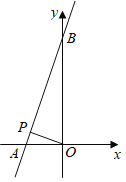
【题目】如图,已知直线![]() 的函数表达式为
的函数表达式为![]() ,与
,与![]() 轴交点为
轴交点为![]() ,与
,与![]() 轴交点为
轴交点为![]() .
.
(1)求![]() 两点的坐标;
两点的坐标;
(2)若点![]() 为线段
为线段![]() 上的一个动点,
上的一个动点,![]() 为坐标原点,是否存在点
为坐标原点,是否存在点![]() ,使
,使![]() 的值最小?若存在,求出
的值最小?若存在,求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
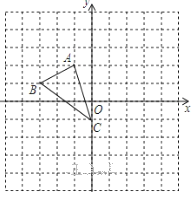
【题目】如图,在平面直角坐标系网格中,△ABC的顶点都在格点上,点C坐标(0,-1).
![]() 作出△ABC 关于原点对称的△A1B1C1,并写出点A1的坐标;
作出△ABC 关于原点对称的△A1B1C1,并写出点A1的坐标;
![]() 把△ABC 绕点C逆时针旋转90°,得△A2B2C2,画出△A2B2C2,并写出点A2的坐标;
把△ABC 绕点C逆时针旋转90°,得△A2B2C2,画出△A2B2C2,并写出点A2的坐标;
(3)直接写出△A2B2C2的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解我县中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图所示.请根据图表信息解答下列问题.
组别 | 分数段(分) | 频数 | 百分率(%) |
A组 | 60≤x<70 | 30 | 10 |
B组 | 70≤x<80 | 90 | n |
C组 | 80≤x<90 | m | 40 |
D组 | 90≤x<100 | 60 | 20 |
(1)样本容量a= ,表中m= ,n= ;
(2)补全频数分布直方图;
(3)若成绩在80分以上(包括80分)为“优”等,请你估计我县参加“科普知识”竞赛的1.5万名学生中成绩是“优”等的约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察后填空:①(x﹣1)(x+1)=x2﹣1; ②(x﹣1)(x2+x+1)=x3﹣1; ③(x﹣1)(x3+x2+x+1)=x4﹣1.
(1)填空:(x﹣1)(x99+x98+x97+…+x+1)= .
(2)请利用上面的结论计算:
①(﹣2)50+(﹣2)49+(﹣2)48+…+(﹣2)+1; ②若x3+x2+x+1=0,求x2016的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学学习过程中,通常是利用已有的知识与经验,通过对研究对象进行观察、实验、推理、抽象概括,发现数学规律,揭示研究对象的本质特征.比如在学习“同底数幂的乘法法则”过程中,利用有理数的乘方概念和乘法结合律,可由“特殊”抽象概括出“一般”,具体如下22×23=25,23×24=27,22×26=28…→2m2n=2m+n…→aman=am+n(m、n都是正整数)我们亦知: ![]() ,
, ![]() ,
, ![]() ,
, ![]() …
…
(1)请你根据上面的材料,用字母a、b、c归纳出a、b、c(a>b>0,c>0)之间的一个数学关系式.
(2)请尝试说明(1)中关系式的正确性.
(3)试用(1)中你归纳的数学关系式,解释下面生活中的一个现象:“若m克糖水里含有n克糖,再加入k克糖(仍不饱和),则糖水更甜了”
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,对角线AC,BD交于点O,折叠正方形ABCD,使AB边落在AC上,点B落在点H处,折痕AE分别交BC于点E,交BO于点F,连结FH,则下列结论(1)AD=DF;(2)![]() =
=![]() ;(3)
;(3)![]() =
=![]() ﹣1;(4)四边形BEHF为菱形.正确的有几个( )
﹣1;(4)四边形BEHF为菱形.正确的有几个( )
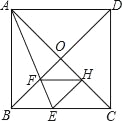
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
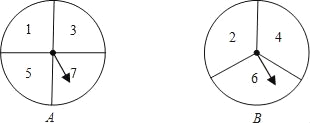
【题目】如图,有A、B两个转盘,其中转盘A被分成4等份,转盘B被分成3等份,并在每一份内标上数字.现甲、乙两人同时各转动其中一个转盘,转盘停止后(当指针指在边界线上时视为无效,重转),若将A转盘指针指向的数字记为x,B转盘指针指向的数字记为y,从而确定点P的坐标为P(x,y).
(1)请用列表或画树状图的方法写出所有可能得到的点P的坐标;
(2)计算点P在函数y=![]() 图象上的概率.
图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点坐标分别为A(﹣6,0),B(4,0),C(0,8),把△ABC沿直线BC翻折,点A的对应点为D,抛物线y=ax2﹣10ax+c经过点C,顶点M在直线BC上.

(1)证明四边形ABCD是菱形,并求点D的坐标;
(2)求抛物线的对称轴和函数表达式;
(3)在抛物线上是否存在点P,使得△PBD与△PCD的面积相等?若存在,直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,对角线AC、BD相交于点O,设锐角∠AOB=α,将△DOC按逆时针方向旋转得到△D′OC′(0°<旋转角<90°)连接AC′、BD′,AC′与BD′相交于点M.

(1)、当四边形ABCD为矩形时,如图1.求证:△AOC′≌△BOD′.
(2)、当四边形ABCD为平行四边形时,设AC=kBD,如图2.
①猜想此时△AOC′与△BOD′有何关系,证明你的猜想;
②探究AC′与BD′的数量关系以及∠AMB与α的大小关系,并给予证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com