
【题目】解下列不等式(组)
(1)3x+8≤5x-12
(2)2x<1-x≤x+5,并写出它的所有整数解.
(3)![]()
(4)
【答案】(1)x≥10;(2)-2≤x<![]() ,它的所有整数解是:-2,-1,0;(3)x>
,它的所有整数解是:-2,-1,0;(3)x>![]() ;(4)无解.
;(4)无解.
【解析】
(1)不等式的步骤,移项、合并同类项、系数化1,求解即可;
(2)把2x<1-x≤x+5化为![]() ,再解出两个不等式各自的解,即可得到不等式组的解集;
,再解出两个不等式各自的解,即可得到不等式组的解集;
(3)等式去分母,去括号,移项,合并同类项,化系数为1即可;
(4)解出每一个不等式,然后求解集的公共部分即可.
(1)3x+8≤5x-12
3x-5x≤-12-8
-2x≤-20
x≥10
(2)2x<1-x≤x+5,并写出它的所有整数解.
可变形为:
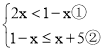
解①得:x<![]()
解②得:x≥-2
所以该不等式组的解集是-2≤x<![]()
它的所有整数解是:-2,-1,0
(3)![]()
不等式两边同乘以6,得3(2x+1)-2(x-2)>6
去括号,得6x+3-2x+4>6
移项,得6x-2x>6-3-4
合并同类项,得4x>-1
系数化成1,得x>![]()
(4)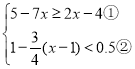
解①得:x≤1
解②得:x>![]()
所以该不等式组无解


科目:初中数学 来源: 题型:
【题目】为响应市委、市政府创建“森林城市”的号召,某中学在校园内计划种植柳树和银杏树.已知购买2棵柳树苗和3棵银杏树苗共需1800元,购买4棵柳树苗和1棵银杏树苗共需1100元.
(1)求每棵柳树苗和每棵银杏树苗各多少钱?
(2)该校计划购买两种树苗共100棵,并且银杏树苗的数量不少于柳树苗的![]() ,请设计出最省钱的购买方案,并说明理由.
,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
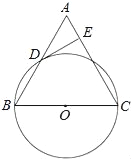
【题目】已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)求证:点D是AB的中点;
(2)判断DE与⊙O的位置关系,并证明你的结论;
(3)若⊙O的直径为18,cosB=![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
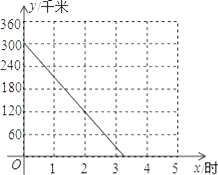
【题目】A、B两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往B城,乙车驶往A城,甲车在行驶过程中速度始终不变.甲车距B城高速公路入口处的距离y(千米)与行驶时间x(时)之间的关系如图.
(1)求y关于x的表达式;
(2)已知乙车以60千米/时的速度匀速行驶,设行驶过程中,两车相距的路程为s(千米).请直接写出s关于x的表达式;
(3)当乙车按(2)中的状态行驶与甲车相遇后,速度随即改为a(千米/时)并保持匀速行驶,结果比甲车晚40分钟到达终点,求乙车变化后的速度a.在下图中画出乙车离开B城高速公路入口处的距离y(千米)与行驶时间x(时)之间的函数图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OABC是菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度向右平移,设直线l与菱形OABC的两边分别交于点M,N(点M在点N的上方),若△OMN的面积为S,直线l的运动时间为t 秒(0≤t≤4),则能大致反映S与t的函数关系的图象是( )
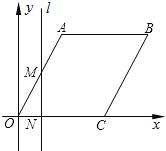
A. B.
B.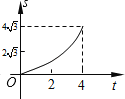
C. D.
D.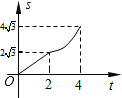
查看答案和解析>>
科目:初中数学 来源: 题型:
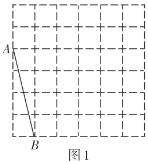
【题目】如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.利用正方形网络可以画出长度为无理数的线段,如图1中![]() .请参考此方法按下列要求作图:
.请参考此方法按下列要求作图:
(1)在图1中以格点为顶点画一个面积为17的正方形![]() ,并标出字母;
,并标出字母;
(2)在图2中以格点为顶点画一个三角形![]() ,使
,使![]() ,
,![]() ,
,![]() ,并标出字母;
,并标出字母;
(3)猜想![]() 是何种特殊三角形.并说明理由.
是何种特殊三角形.并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题解决:
如图1,已知正方形![]() ,
,![]() ,把含
,把含![]() (
(![]() )的直角三角板的一个锐角顶点和点
)的直角三角板的一个锐角顶点和点![]() 重合,三角板和正方形的
重合,三角板和正方形的![]() ,
,![]() 两边分别相交于
两边分别相交于![]() ,
,![]() 两点.
两点.
(1)当![]() 时,求
时,求![]() 的长;
的长;
探究发现:
(2)在图1的基础上,试探究![]() ,
,![]() ,
,![]() 有怎样的数量关系,请写出猜想,并给予证明.
有怎样的数量关系,请写出猜想,并给予证明.
类比延伸:
(3)如图2,若三角板和正方形![]() ,
,![]() 两边的延长线分别相交于
两边的延长线分别相交于![]() ,
,![]() 两点,请直接写出
两点,请直接写出![]() ,
,![]() ,
,![]() 存在的数量关系.
存在的数量关系.


查看答案和解析>>
科目:初中数学 来源: 题型:
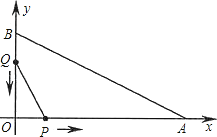
【题目】如图,在平面直角坐标系中,已知OA=12厘米,OB=6厘米.点P从点O开始沿OA边向点A以1厘米/秒的速度移动;点Q从点B开始沿BO边向点O以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6),那么,当t为何值时,△POQ与△AOB相似?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com