
【题目】在△ABC中,∠ACB=60°,CE为△ABC的角平分线,AC边上的高BD与CE所在的直线交于点F,若∠ABD:∠ACF=2:3,则∠BEC的度数为_____.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图:已知AB是⊙O的直径,BC是⊙O的切线,OC与⊙O相交于点D,连结AD并延长,与BC相交于点E。
(1)若BC=![]() ,CD=1,求⊙O的半径;
,CD=1,求⊙O的半径;
(2)取BE的中点F,连结DF,求证:DF是⊙O的切线。
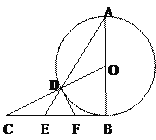
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(π﹣3)0﹣(![]() )﹣2+(﹣1)2n
)﹣2+(﹣1)2n
(2)(m2)n(mn)3÷mn﹣2
(3)x(x2﹣x﹣1)
(4)(﹣3a)2a4+(﹣2a2)3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产![]() 两种设备,已知每台
两种设备,已知每台![]() 种设备的成本是
种设备的成本是![]() 种设备的1.5倍,公司若投入6万元生产
种设备的1.5倍,公司若投入6万元生产![]() 种设备,投人15万元生产
种设备,投人15万元生产![]() 种设备,则可生产两种设备共40台.请解答下列问题:
种设备,则可生产两种设备共40台.请解答下列问题:
(1)![]() 两种设备每台的成本分别是多少万元?
两种设备每台的成本分别是多少万元?
(2)若![]() 两种设备每台的售价分别是5000元、9000元,公司决定生产两种设备共50台,且其中
两种设备每台的售价分别是5000元、9000元,公司决定生产两种设备共50台,且其中![]() 种设备至少生产10台,计划销售后获利不低于12万元,请问采用哪种生产方案公司所获利润最大?并求出最大利润.
种设备至少生产10台,计划销售后获利不低于12万元,请问采用哪种生产方案公司所获利润最大?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课间,小明拿着老师的等腰三角板玩,不小心掉到两墙之间,如图.
(1)求证:△ADC≌△CEB;
(2)从三角板的刻度可知AC=25cm,请你帮小明求出砌墙砖块的厚度a的大小(每块砖的厚度相等).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在某场足球比赛中,球员甲从球门底部中心点O的正前方10m处起脚射门,足球沿抛物线飞向球门中心线;当足球飞离地面高度为3m时达到最高点,此时足球飞行的水平距离为6m.已知球门的横梁高为2.44m.
(1)在如图所示的平面直角坐标系中,问此飞行足球能否进球门?(不计其它情况)
(2)守门员乙站在距离球门2m处,他跳起时手的最大摸高为2.52m,他能阻止球员甲的此次射门吗?如果不能,他至少后退多远才能阻止球员甲的射门?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:
(1)则样本容量是 ,并补全直方图;
(2)该年级共有学生500人,请估计全年级在这天里发言次数不少于12的次数;
(3)已知A组发言的学生中恰有1位女生,E组发言的学生中有2位男生,现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率.
发言次数n | |
A | 0≤n<3 |
B | 3≤n<6 |
C | 6≤n<9 |
D | 9≤n<12 |
E | 12≤n<15 |
F | 15≤n<18 |

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级组织有奖知识竞赛,派小明去购买A、B两种品牌的钢笔作为奖品.已知一支A品牌钢笔的价格比一支B品牌钢笔的价格多5元,且买100元A品牌钢笔与买50元B品牌钢笔数目相同.
(1)求A、B两种品牌钢笔的单价分别为多少元?
(2)根据活动的设奖情况,决定购买A、B两种品牌的钢笔共100支,如果设购买A品牌钢笔的数量为n支,购买这两种品牌的钢笔共花费y元.
①直接写出y(元)关于n(支)的函数关系式;
②如果所购买A品牌钢笔的数量不少于B品牌钢笔数量的![]() ,请你帮助小明计算如何购买,才能使所花费的钱最少?此时花费是多少?
,请你帮助小明计算如何购买,才能使所花费的钱最少?此时花费是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com