
 如图,正方形ABCD的边长为2,△ABE是等边三角形.
如图,正方形ABCD的边长为2,△ABE是等边三角形.| 3 |
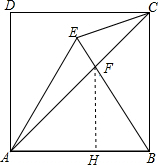 解:(1)∵△ABE是等边三角形,
解:(1)∵△ABE是等边三角形,| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 2 |
| 6 |
| 3 |
| 2 |
| 6 |


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:
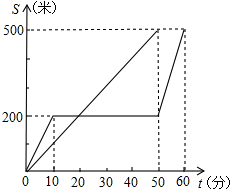 “龟兔赛跑”是同学们熟悉的寓言故事.如图所示,表示了寓言中的龟、兔的路程S和时间t的关系(其中直线段表示乌龟,折线段表示兔子),请看图回答问题.
“龟兔赛跑”是同学们熟悉的寓言故事.如图所示,表示了寓言中的龟、兔的路程S和时间t的关系(其中直线段表示乌龟,折线段表示兔子),请看图回答问题.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,一次函数y1=kx+b的图象与反比例函数y2=
如图,一次函数y1=kx+b的图象与反比例函数y2=| m |
| x |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com