
����Ŀ������ij����Ʒ������һ���Ʒ����֪����Ʒ�������ɱ�Ϊÿ��60Ԫ�����г����з��֣��ÿ��Ʒÿ���������y���������ۼ�x��Ԫ��֮����������±���ʾ��һ�κ�����ϵ��
�ۼ�x��Ԫ�� | �� | 70 | 90 | �� |
������y������ | �� | 3000 | 1000 | �� |
������=���ۼ۩��ɱ��ۣ�����������
��1����������y���������ۼ�x��Ԫ��֮��ĺ�����ϵʽ��
��2������Ϊ��ζ��۲���ʹ����Ʒ��ÿ���õ�����Ϊ40000Ԫ��
���𰸡�������Ϊ80Ԫʱ����ʹ����Ʒ��ÿ���õ�����Ϊ40000Ԫ��
�������������������1����һ�κ�����һ��ʽy=kx+b������70��3000����90��1000�����뼴����ã�
��2�����յ�����ϵ������=������-�ɱ��������������г�������ڶ��۵ĺ������̣���⼴�ɣ�
�����������1����һ�κ�����ϵʽΪy=kx+b�����������
![]()
��֮��k=��100��b=10000
��������һ�κ�����ϵʽΪy=��100x+10000��x��0��
��2��������ã�x��60������100x+10000��=40000
��x2��160x+6400=0�����ԣ�x��80��2=0
����x1=x2=80
�𣺵�����Ϊ80Ԫʱ����ʹ����Ʒ��ÿ���õ�����Ϊ40000Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ֻ���ÿ���ӯ����ÿ���������һ���Ĺ�ϵ��ÿ��ֲ3��ʱ��ƽ��ÿ��ӯ��4Ԫ����ÿ������1�꣬ƽ��ÿ��ӯ������0.5Ԫ��Ҫʹÿ���ӯ���ﵽ15Ԫ��ÿ��Ӧ��ֲ�����ꣿ��ÿ���ֲx�꣬������г��ķ����ǣ� ��
A.��3+x����4��0.5x��=15
B.��x+3����4+0.5x��=15
C.��x+4����3��0.5x��=15
D.��x+1����4��0.5x��=15
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣������ε����߳��ֱ�Ϊm+1��m+7����ͼ�ڣ������ε�����
���ֱ�Ϊm+2��m+4��(����mΪ������)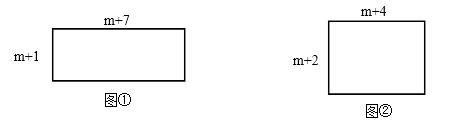
��1��ͼ���г����ε���� ![]() =
=
ͼ���г����ε���� ![]() =
=
�Ƚϣ� ![]()
![]() (�����������������)
(�����������������)
��2������һ�����Σ����ܳ���ͼ���еij������ܳ���ȣ���
���������εı߳�(�ú�m�Ĵ���ʽ��ʾ)��
����̽��������������� ![]() ��ͼ���г��������
��ͼ���г�������� ![]() �IJ�(��
�IJ�(�� ![]() -
- ![]() )��һ������,������������
)��һ������,������������
��3����(1)�������£���ij��ͼ�ε�������� ![]() ��
�� ![]() ֮��(������
֮��(������ ![]() ��
�� ![]() )�������Ϊ����������������ֵ����ֻ��10������m��ֵ��
)�������Ϊ����������������ֵ����ֻ��10������m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У���ACB=90�㣬��A=50�㣬�����۵���ʹ��A���ڱ�CB��A�䴦���ۺ�ΪCD�����A��DB=�� �� 
A.40��
B.30��
C.20��
D.10��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCDΪƽ���ı��Σ��ӳ�AD��E��ʹDE=AD������EB��EC��DB.����һ������������ʹ�ı���DBCEΪ���ε��ǣ� ��

A. AB=BE B. BE��CD C. ��ADB=900 D. CE��DE
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC������AB��BC��CA���ֱ���20��30��40����������ƽ���߽���ABC�ֳ����������Σ���S��ABO��S��BCO��S��CAO���� �� 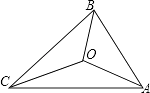
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�����ı���ABCD�У�AB��AD����BAD����BCD��90�㣬AH��BC��H��AH��CH��5�����ı���ABCD������ǣ��� ��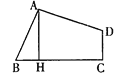
A.15
B.20
C.25
D.��ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ʽ��������ȫƽ����ʽ������ʽ�ֽ���ǣ� ��
A.x2+x+1
B.x2��6x+9
C.x2��1
D.x2+2x��1
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com