
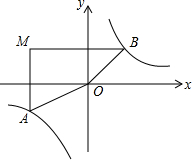
 如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数y=$\frac{2}{x}$的图象交于A、B两点,则四边形MAOB的面积为8.
如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数y=$\frac{2}{x}$的图象交于A、B两点,则四边形MAOB的面积为8. 分析 设点A的坐标为(a,b),点B的坐标为(c,d),根据反比例函数y=$\frac{2}{x}$的图象过A,B两点,所以ab=2,cd=2,进而得到S△AOC=$\frac{1}{2}$|ab|=1,S△BOD=$\frac{1}{2}$|cd|=1,S矩形MCDO=3×2=6,根据四边形MAOB的面积=S△AOC+S△BOD+S矩形MCDO,即可解答.
解答 解:如图,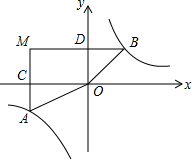
设点A的坐标为(a,b),点B的坐标为(c,d),
∵反比例函数y=$\frac{2}{x}$的图象过A,B两点,
∴ab=2,cd=2,
∴S△AOC=$\frac{1}{2}$|ab|=1,S△BOD=$\frac{1}{2}$|cd|=1,
∵点M(-3,2),
∴S矩形MCDO=3×2=6,
∴四边形MAOB的面积=S△AOC+S△BOD+S矩形MCDO=1+1+6=8,
故答案为:8.
点评 本题主要考查反比例函数的对称性和比例系数k的几何意义,根据条件得出S△AOC=$\frac{1}{2}$|ab|=1,S△BOD=$\frac{1}{2}$|cd|=1是解题的关键,注意k的几何意义的应用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
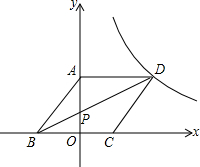 如图,边长为a的菱形ABCD的顶点D在反比例函数y=$\frac{k}{x}$(x>0)的图象上,A、C两点的坐标分别为(0,4)和(2,0).
如图,边长为a的菱形ABCD的顶点D在反比例函数y=$\frac{k}{x}$(x>0)的图象上,A、C两点的坐标分别为(0,4)和(2,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
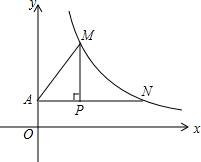 如图,点P的坐标为(2,$\frac{3}{2}$),过点P作x轴的平行线交y轴于点A,交双曲线y=$\frac{k}{x}$(x>0)于点N;作PM⊥AN交双曲线y=$\frac{k}{x}$(x>0)于点M,连接AM.已知PN=4.
如图,点P的坐标为(2,$\frac{3}{2}$),过点P作x轴的平行线交y轴于点A,交双曲线y=$\frac{k}{x}$(x>0)于点N;作PM⊥AN交双曲线y=$\frac{k}{x}$(x>0)于点M,连接AM.已知PN=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
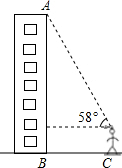 小明搬了新家,他想利用所学知识测量他家所在这栋楼的高度BA,如图所示,小明所站位置与这栋大楼的距离CB为30m,他仰望楼顶A处,仰角约为58°,已知小明身高为1.68m,请问这栋楼有多高?若每一层按照2.9m计算,你知道小明家所在的这栋楼共有多少层吗?(结果精确到0.1米)
小明搬了新家,他想利用所学知识测量他家所在这栋楼的高度BA,如图所示,小明所站位置与这栋大楼的距离CB为30m,他仰望楼顶A处,仰角约为58°,已知小明身高为1.68m,请问这栋楼有多高?若每一层按照2.9m计算,你知道小明家所在的这栋楼共有多少层吗?(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
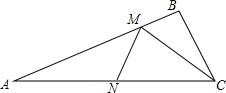 如图:△ABC中,AC=6,∠BAC=22.5°,点M、N分别是射线AB和AC上动点,则CM+MN的最小值是( )
如图:△ABC中,AC=6,∠BAC=22.5°,点M、N分别是射线AB和AC上动点,则CM+MN的最小值是( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
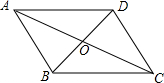 如图,?ABCD的对角线AC、BD相交于点O,增加下列条件后,?ABCD不一定是菱形的是( )
如图,?ABCD的对角线AC、BD相交于点O,增加下列条件后,?ABCD不一定是菱形的是( )| A. | DC=BC | B. | AC⊥BD | C. | AB=BD | D. | ∠ADB=∠CDB |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在?ABCD中,E是AD上一点,连接CE并延长交BA的延长线于点F,则下列结论中错误的是( )
如图,在?ABCD中,E是AD上一点,连接CE并延长交BA的延长线于点F,则下列结论中错误的是( )| A. | $\frac{AF}{AB}$=$\frac{AE}{DE}$ | B. | $\frac{AF}{CD}$=$\frac{AE}{BC}$ | C. | $\frac{AF}{AB}=\frac{EF}{CE}$ | D. | $\frac{DE}{AE}=\frac{CE}{EF}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y3>y1>y2 | D. | y3>y2>y1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com