
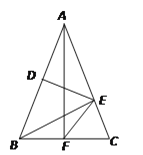
【题目】如图,△ABC中,AB=AC,DE垂直平分AB,BE⊥AC,AF⊥BC,则∠EFC=____°.
【答案】45.
【解析】试题分析:根据线段垂直平分线上的点到线段两端点的距离相等可得AE=BE,然后求出△ABE是等腰直角三角形,根据等腰直角三角形的性质求出∠BAE=∠ABE=45°,再根据等腰三角形两底角相等求出∠ABC,然后求出∠CBE,根据等腰三角形三线合一的性质可得BF=CF,根据直角三角形斜边上的中线等于斜边的一半可得BF=EF,根据等边对等角求出∠BEF=∠CBE,然后根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
解:∵DE垂直平分AB,
∴AE=BE,
∵BE⊥AC,
∴△ABE是等腰直角三角形,
∴∠BAE=∠ABE=45°,
又∵AB=AC,
∴∠ABC=![]() (180°﹣∠BAC)=
(180°﹣∠BAC)=![]() (180°﹣45°)=67.5°,
(180°﹣45°)=67.5°,
∴∠CBE=∠ABC﹣∠ABE=67.5°﹣45°=22.5°,
∵AB=AC,AF⊥BC,
∴BF=CF,
∵EF=![]() BC(直角三角形斜边中线等于斜边的一半),
BC(直角三角形斜边中线等于斜边的一半),
∴BF=EF=CF,
∴∠BEF=∠CBE=22.5°,
∴∠EFC=∠BEF+∠CBE=22.5°+22.5°=45°.
故答案为:45.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
【题目】【问题情境】一节数学课后,老师布置了一道课后练习题:
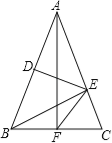
如图:已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,点E、F分别在A和BC上,∠1=∠2,FG⊥AB于点G,求证:△CDE≌△EGF.
(1)阅读理解,完成解答
本题证明的思路可用下列框图表示: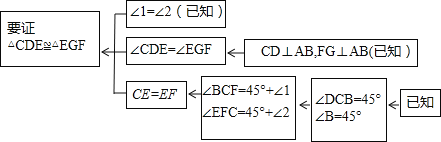
根据上述思路,请你完整地书写这道练习题的证明过程;
(2)特殊位置,证明结论
若CE平分∠ACD,其余条件不变,求证:AE=BF;
(3)知识迁移,探究发现
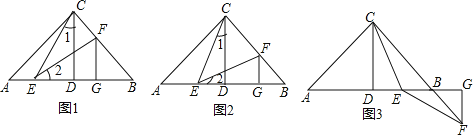
如图,已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,若点E是DB的中点,点F在直线CB上且满足EC=EF,请直接写出AE与BF的数量关系.(不必写解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验中学现有学生2 870人,学校为了进一步丰富学生课余生活,拟调查各兴趣小组活动情况,为此校学生会委托小容、小易进行一次随机抽样调查.根据采集到的数据,小容绘制的统计图1,小易绘制的统计图2(不完整)如下:
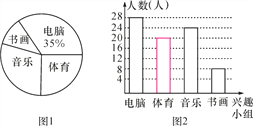
请你根据统计图1、2中提供的信息,解答下列问题:
(1)写出2条有价值信息(不包括下面要计算的信息);
(2)这次抽样调查的样本容量是多少?在图2中,请将小易画的统计图中的“体育”部分的图形补充完整;
(3)爱好“书画”的人数占被调查人数的百分数是多少?估计实验中学现有的学生中,有多少人爱好“书画”?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在超市买一食品,外包装上印有“总净含量(300±5)g”的字样。小明拿去称了一下,发现只有297g.则食品生产厂家 (填“有”或“没有”)欺诈行为。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.
(1)求A,B两种品牌的足球的单价.
(2)求该校购买20个A品牌的足球和2个B品牌的足球的总费用.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形的两边长分别为3和6,第三边的长是方程x2-6x+8=0的一个根,则这个三角形的周长是( )
A. 9 B. 11 C. 13 D. 11或13
查看答案和解析>>
科目:初中数学 来源: 题型:
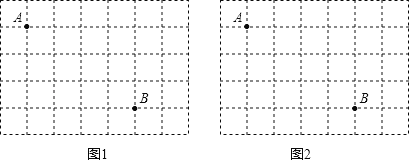
【题目】图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,点A和点B在小正方形的顶点上.
(1)在图1中画出△ABC(点C在小正方形的顶点上),使△ABC为直角三角形(画一个即可);
(2)在图2中画出△ABD(点D在小正方形的顶点上),使△ABD为等腰三角形(画一个即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com