
【题目】【问题情境】一节数学课后,老师布置了一道课后练习题:
如图:已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,点E、F分别在A和BC上,∠1=∠2,FG⊥AB于点G,求证:△CDE≌△EGF.
(1)阅读理解,完成解答
本题证明的思路可用下列框图表示: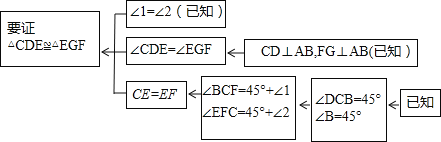
根据上述思路,请你完整地书写这道练习题的证明过程;
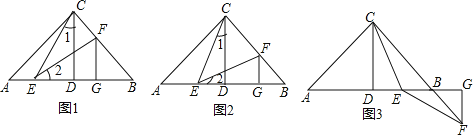
(2)特殊位置,证明结论
若CE平分∠ACD,其余条件不变,求证:AE=BF;
(3)知识迁移,探究发现
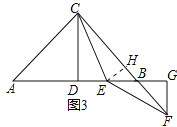
如图,已知在Rt△ABC中,AC=BC,∠ACB=90°,CD⊥AB于点D,若点E是DB的中点,点F在直线CB上且满足EC=EF,请直接写出AE与BF的数量关系.(不必写解答过程)
【答案】(1)、证明过程见解析;(2)、证明过程见解析;(3)、AE=![]() BF.
BF.
【解析】
试题分析:(1)、先证明CE=EF,根据AAS即可证明△CDE≌△EGF;(2)、先证∠ACE=∠2,再证明△ACE≌△BEF,即可得出AE=BF;(3)、作EH⊥BC与H,设DE=x,求出AE=3x,再证出BF=![]() x,即可得出结论.
x,即可得出结论.
试题解析:(1)、∵AC=BC,∠ACB=90°, ∴∠A=∠B=45°, ∵CD⊥AB, ∴∠CDB=90°,
∴∠DCB=45°, ∵∠ECF=∠DCB+∠1=45°+∠1,∠EFC=∠B+∠2=45°+∠2,∠1=∠2, ∴∠ECF=∠EFC,
∴CE=EF, ∵CD⊥AB,FG⊥AB, ∴∠CDE=∠EGF=90°,
在△CDE和△EGF中,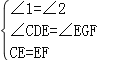 ,∴△CDE≌△EGF(AAS);
,∴△CDE≌△EGF(AAS);
(2)、由(1)得:CE=EF,∠A=∠B, ∵CE平分∠ACD, ∴∠ACE=∠1, ∵∠1=∠2,∴∠ACE=∠2,
在△ACE和△BEF中, ,∴△ACE≌△BEF(AAS),∴AE=BF;
,∴△ACE≌△BEF(AAS),∴AE=BF;
(3)、AE=![]() BF,作EH⊥BC与H,如图3所示:
BF,作EH⊥BC与H,如图3所示:
设DE=x,根据题意得:BE=DE=x,AD=BD=2x,CD=AD=2x,AE=3x, 根据勾股定理得:BC=AC=2![]() x,
x,
∵∠ABC=45°,EH⊥BC, ∴BH=![]() x, ∴CH=BC﹣BH=
x, ∴CH=BC﹣BH=![]() x, ∵EC=EF, ∴FH=CH=
x, ∵EC=EF, ∴FH=CH=![]() x,
x,
∴BF=![]() x﹣
x﹣![]() x=
x=![]() x, ∴
x, ∴![]() , ∴AE=
, ∴AE=![]() BF.
BF.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某学校设计了如图1-4-6的一个雕塑,取名“阶梯”,现在工人师傅打算用油漆喷刷所有的暴露面.经测量,已知每个小正方体的棱长为0.5 m,请你帮助工人师傅算一下,需喷刷油漆的总面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
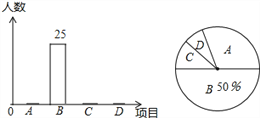
【题目】某校的20年校庆举办了四个项目的比赛,现分别以A,B,C,D表示它们.要求每位同学必须参加且限报一项.以701班为样本进行统计,并将统计结果绘制如下两幅统计图,其中参加A项目的人数比参加C与D项目人数的总和多1人,参加D项目的人数比参加A项目的人数少11人.请你结合图中所给出的信息解答下列问题:
(1)求出全班总人数;
(2)求出扇形统计图中参加D项目比赛的学生所在的扇形圆心角的度数;
(3)若该校7年级学生共有200人,请你估计这次活动中参加A和B项目的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某摩托车厂本周内计划每日生产300辆摩托车,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(增加的车辆数为正数,减少的车辆数为负数)

(1)本周三生产了摩托车 辆;
(2)本周总生产量与计划生产量相比,是增加还是减少?
(3)产量最多的一天比产量最少的一天多生产了多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程数.“燃油效率”越高表示汽车每消耗1升汽油行驶的里程数越多;“燃油效率”越低表示汽车每消耗1升汽油行驶的里程数越少.如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列说法中,正确的是( )
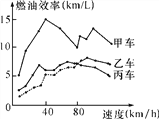
A. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
B. 以低于80 km/h的速度行驶时,行驶相同路程,三辆车中,乙车消耗汽油最少
C. 以高于80 km/h的速度行驶时,行驶相同路程,丙车比乙车省油
D. 以80 km/h的速度行驶时,行驶100公里,甲车消耗的汽油量约为10升
查看答案和解析>>
科目:初中数学 来源: 题型:
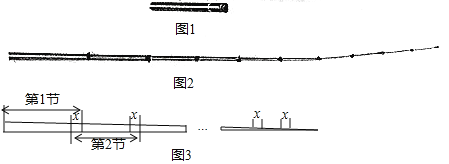
【题目】如图是一根可伸缩的鱼竿,鱼竿是用10节大小不同的空心套管连接而成.闲置时鱼竿可收缩,完全收缩后,鱼竿长度即为第1节套管的长度(如图1所示):使用时,可将鱼竿的每一节套管都完全拉伸(如图2所示).图3是这跟鱼竿所有套管都处于完全拉伸状态下的平面示意图.已知第1节套管长50cm,第2节套管长46cm,以此类推,每一节套管均比前一节套管少4cm.完全拉伸时,为了使相邻两节套管连接并固定,每相邻两节套管间均有相同长度的重叠,设其长度为xcm.
(1)请直接写出第5节套管的长度;
(2)当这根鱼竿完全拉伸时,其长度为311cm,求x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com