
����Ŀ��ijУ��20��У��ٰ����ĸ���Ŀ�ı������ֱַ���A��B��C��D��ʾ���ǣ�Ҫ��ÿλͬѧ����μ����ޱ�һ���701��Ϊ��������ͳ�ƣ�����ͳ�ƽ��������������ͳ��ͼ�����вμ�A��Ŀ�������Ȳμ�C��D��Ŀ�������ܺͶ�1�ˣ��μ�D��Ŀ�������Ȳμ�A��Ŀ��������11�ˣ�������ͼ������������Ϣ����������⣺
��1�����ȫ����������
��2���������ͳ��ͼ�вμ�D��Ŀ������ѧ�����ڵ�����Բ�ĽǵĶ�����
��3������У7�꼶ѧ������200�ˣ����������λ�вμ�A��B��Ŀ��ѧ�����ж����ˣ�
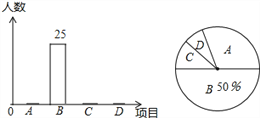
���𰸡���1������Ϊ��50��
��2���μ�D��Ŀ��ѧ����ռ����Բ�Ľ�Ϊ14.4�㣻
��3���μ�A��B��Ŀ��ѧ��������152�ˣ�
�������������������1������B�������Ϊ25ռ50%������2��25����������2���������⣬��μ�D��Ŀ������Ϊx�ˣ�C��Ŀ������Ϊy�ˣ��г������飬���D��Ŀ����������D��Ŀ��������������360������Ϊ�μ�D��Ŀ��ѧ����ռ����Բ�ĽǶ�������3�����ݲμ�A��B��Ŀ��ѧ������=7�꼶ѧ��������A��B��Ŀ��ѧ�������ٷֱȣ�
�����������1��������2��25=50��
��2����μ�D��Ŀ������Ϊx�ˣ�C��Ŀ������Ϊy�ˣ���A��Ŀ������Ϊ��x+11���ˣ�
������ã� ![]()
��ã� ![]() ��
��
���Բμ�D��Ŀ������2�ˣ�
�μ�D��Ŀ��ѧ����ռ����Բ�Ľǣ� ![]() ��360��=14.4����
��360��=14.4����
��3���μ�A��B��Ŀ��ѧ�������� ![]() =152���ˣ���
=152���ˣ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��ֱ������A��B��C���㣬AB=6cm��BC=2cm����P��Q�ֱ����߶�AB��BC���е㣬��PQ= ______ cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A����3��y1����B��2��y2����������y=x2��5x�ϣ���y1 y2 �� �����������������=����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������y=��m+1��x �� y��x���������С����m��ȡֵ��Χ�ǣ�������
A.m��-1
B.m��-1
C.m��-1
D.m��-1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
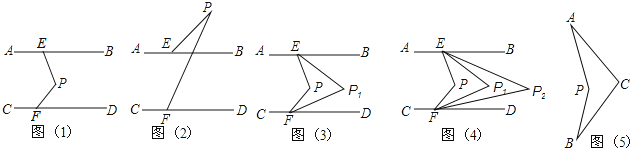
����Ŀ����ͼ��1����ֱ��AB��CD����P����ƽ����֮�䣬��E��AB�ϣ���F��CD�ϣ�����PE��PF��
��1����PEB����PFD����EPF�����������ϵ�� ����˵�����ɣ�
��2����ͼ��2��������P��ֱ��AB�ϲ�ʱ����PEB����PFD����EPF�����������ϵ�� ������˵�����ɣ�
��3����ͼ��3������ͼ��1�������ϣ�P![]() Eƽ�֡�PEB��P
Eƽ�֡�PEB��P![]() Fƽ�֡�PFD�������PEB=x�㣬��PFD=y�㣮���P
Fƽ�֡�PFD�������PEB=x�㣬��PFD=y�㣮���P![]() =______����x��y�Ĵ���ʽ��ʾ������P
=______����x��y�Ĵ���ʽ��ʾ������P![]() Eƽ�֡�P
Eƽ�֡�P![]() EB��P
EB��P![]() Fƽ�֡�P
Fƽ�֡�P![]() FD���ɵá�P
FD���ɵá�P![]() ��P
��P![]() Eƽ�֡�P
Eƽ�֡�P![]() EB��P
EB��P![]() Fƽ�֡�P
Fƽ�֡�P![]() FD���ɵá�P
FD���ɵá�P![]() ��������ƽ����ȥ�����P
��������ƽ����ȥ�����P![]() =______��
=______��
��4���Ƽ�����ϣ�����ͬѧ������һ��ͼ��5���ġ������ڡ������������֡�PAC=28�㣬
��PBC=30�㣬������֪����APB���ACB��������ϵ�����ܸ�������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,BD�ǡ�ABCƽ���ߣ�DE![]() AB��E��AB=36cm,BC=24cm,S��ABC =144cm2,��DE�ij��ǣ� ��
AB��E��AB=36cm,BC=24cm,S��ABC =144cm2,��DE�ij��ǣ� ��

A. 4.8cm B. 4.5cm C. 4 cm D. 2.4cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������龳��һ����ѧ�κ���ʦ������һ���κ���ϰ�⣺
��ͼ����֪��Rt��ABC�У�AC=BC����ACB=90����CD��AB�ڵ�D����E��F�ֱ���A��BC�ϣ���1=��2��FG��AB�ڵ�G����֤����CDE�ա�EGF��
��1���Ķ����⣬��ɽ��
����֤����˼·�������п�ͼ��ʾ��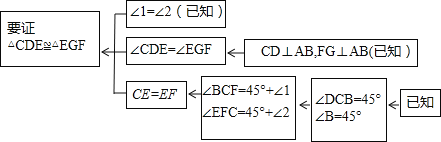
��������˼·��������������д�����ϰ���֤�����̣�
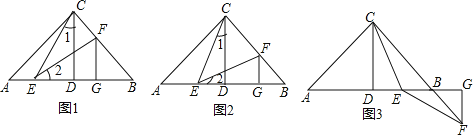
��2������λ�ã�֤������
��CEƽ����ACD�������������䣬��֤��AE=BF��
��3��֪ʶǨ�ƣ�̽������
��ͼ����֪��Rt��ABC�У�AC=BC����ACB=90����CD��AB�ڵ�D������E��DB���е㣬��F��ֱ��CB��������EC=EF����ֱ��д��AE��BF��������ϵ��������д�����̣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com