
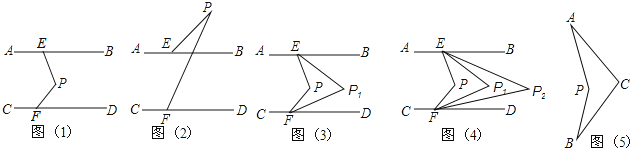
����Ŀ����ͼ��1����ֱ��AB��CD����P����ƽ����֮�䣬��E��AB�ϣ���F��CD�ϣ�����PE��PF��
��1����PEB����PFD����EPF�����������ϵ�� ����˵�����ɣ�
��2����ͼ��2��������P��ֱ��AB�ϲ�ʱ����PEB����PFD����EPF�����������ϵ�� ������˵�����ɣ�
��3����ͼ��3������ͼ��1�������ϣ�P![]() Eƽ�֡�PEB��P
Eƽ�֡�PEB��P![]() Fƽ�֡�PFD�������PEB=x�㣬��PFD=y�㣮���P
Fƽ�֡�PFD�������PEB=x�㣬��PFD=y�㣮���P![]() =______����x��y�Ĵ���ʽ��ʾ������P
=______����x��y�Ĵ���ʽ��ʾ������P![]() Eƽ�֡�P
Eƽ�֡�P![]() EB��P
EB��P![]() Fƽ�֡�P
Fƽ�֡�P![]() FD���ɵá�P
FD���ɵá�P![]() ��P
��P![]() Eƽ�֡�P
Eƽ�֡�P![]() EB��P
EB��P![]() Fƽ�֡�P
Fƽ�֡�P![]() FD���ɵá�P
FD���ɵá�P![]() ��������ƽ����ȥ�����P
��������ƽ����ȥ�����P![]() =______��
=______��
��4���Ƽ�����ϣ�����ͬѧ������һ��ͼ��5���ġ������ڡ������������֡�PAC=28�㣬
��PBC=30�㣬������֪����APB���ACB��������ϵ�����ܸ�������˵�����ɣ�
���𰸡���1����PEB����PFD����P�����������ϵ�ǡ�P=��PEB+��PFD�����ɼ�������
��2����PFD=��PEB+��P
��3����P1=![]() ����Pn=
����Pn=![]()
��4����APB=��C+58��
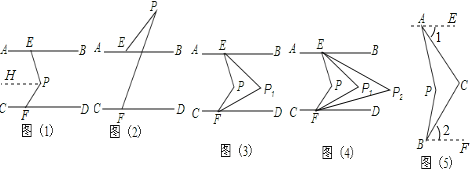
�������������������1������P��PH��AB��CD������ƽ���ߵ����ʣ���ֱ��ƽ�У��ڴ�����ȼ���֤�ã�
��2������P��ֱ��AB��ʱ����P��AB��ƽ���ߣ�ͬ��������ֱ��ƽ�У��ڴ�����ȼ���֤�ã�
��3�����ã�1���Ľ��ۺͽ�ƽ���ߵ����ʼ���д�����ۣ�
��4����A��B�ֱ���ֱ��AE��BF��ʹAE��BF�����ã�1���Ľ��ۼ�����⣮
���������(1)��PEB����PFD����P�����������ϵ�ǡ�P=��PEB+��PFD
�������£�����P��PH��AB��CD
���PEB=��EPH����PFD=��FPH
����EPF=��EPH+��FPH
���EPF=��PEB+��PFD
(2)��ͼ(2)������P��ֱ��AB��ʱ��
��PEB����PFD����P�����������ϵ�ǡ�PFD=��PEB+��P
(����˵������)
(3)��P1=![]() (x+y)��(��x,y�Ĵ���ʽ��ʾ)
(x+y)��(��x,y�Ĵ���ʽ��ʾ)
��Pn=(![]() )n(x+y)��.
)n(x+y)��.
(4)��APB=��C+58.�������£�
��A.B�ֱ���ֱ��AE��BF,ʹAE��BF.
��ͼ,��(1)���ɿ�֪��C=��1+��2.
��APB=��PAE+��PBF=(��PAC+��1)+(��PBC+��2)=��PAC+��PBC+(��1+��2)=��C+58��


 ��������ϵ�д�
��������ϵ�д� ����˼ά����ѵ����ʱ��ѧ��ϵ�д�
����˼ά����ѵ����ʱ��ѧ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
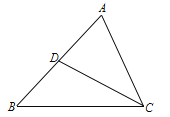
����Ŀ����ͼ������ABC�У�CD��AB���ϵ����ߣ���֪��B��45��tan��ACB��3��AC=![]() ��
��
��1����ABC���������2��sin��ACD��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
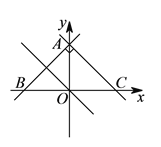
����Ŀ����ƽ��ֱ������ϵ�У���ֱ��y=kx+b������һ�����������ޣ���ֱ��y=bx-k�������������ǣ� ��
A.��һ����B.�ڶ�����C.��������D.��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪��һ�κ���![]() ��
��![]() ��ͼ�����
��ͼ�����![]() ��Գƣ��������Ƕ��壺����
��Գƣ��������Ƕ��壺����![]() ��
��![]() ��Ϊ�����ӡ�������
��Ϊ�����ӡ�������
��![]() ����ֱ��д������
����ֱ��д������![]() �ġ����ӡ�����__________��
�ġ����ӡ�����__________��
��![]() �����һ�ԡ����ӡ�����
�����һ�ԡ����ӡ�����![]() ��
��![]() ��ͼ���ڵ�
��ͼ���ڵ�![]() ������
������![]() �ύ��
�ύ��![]() ��
��![]() ���㣬��ͼ��ʾ����
���㣬��ͼ��ʾ����![]() ����
����![]() �������
�������![]() ������ԡ����ӡ������Ľ���ʽ��
������ԡ����ӡ������Ľ���ʽ��
��![]() ������
������![]() ��
��![]() ���ϵ�һ�����㣬��
���ϵ�һ�����㣬��![]() Ϊ����������ʱ��ֱ��д����
Ϊ����������ʱ��ֱ��д����![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
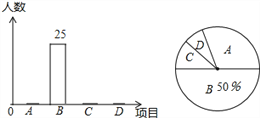
����Ŀ��ijУ��20��У��ٰ����ĸ���Ŀ�ı������ֱַ���A��B��C��D��ʾ���ǣ�Ҫ��ÿλͬѧ����μ����ޱ�һ���701��Ϊ��������ͳ�ƣ�����ͳ�ƽ��������������ͳ��ͼ�����вμ�A��Ŀ�������Ȳμ�C��D��Ŀ�������ܺͶ�1�ˣ��μ�D��Ŀ�������Ȳμ�A��Ŀ��������11�ˣ�������ͼ������������Ϣ����������⣺
��1�����ȫ����������
��2���������ͳ��ͼ�вμ�D��Ŀ������ѧ�����ڵ�����Բ�ĽǵĶ�����
��3������У7�꼶ѧ������200�ˣ����������λ�вμ�A��B��Ŀ��ѧ�����ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ȷֱ�Ϊ6cm��8cm��10cm������ľ����β˳����ӣ����һ��ֱ�������Σ�������¼��ǣ�������
A. ��Ȼ�¼� B. �������¼� C. ����¼� D. ��ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijĦ�г��������ڼƻ�ÿ������300��Ħ�г������ڹ���ʵ�����ݣ�ÿ���ϰ�������һ����ȣ�ʵ��ÿ����������ƻ������������±������ӵij�����Ϊ���������ٵij�����Ϊ������

��1��������������Ħ�г� ����
��2����������������ƻ���������ȣ������ӻ��Ǽ��٣�
��3����������һ��Ȳ������ٵ�һ��������˶�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com