
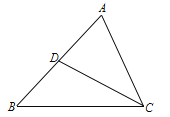
【题目】如图,在△ABC中,CD是AB边上的中线,已知∠B=45,tan∠ACB=3,AC=![]() ,
,
求:(1)△ABC的面积;(2)sin∠ACD的值.
【答案】(1)、6;(2)、![]() .
.
【解析】
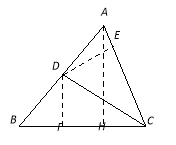
试题分析:(1)、作AH⊥BC,根据Rt△ACH中∠ACB的正切值得出AH的长度,根据等腰直角△ABH得出BH的长度,然后计算面积;(2)、作DE⊥AC,DF⊥BC,根据△ACD的面积求出DE的长度,根据Rt△CDF的勾股定理求出CD的长度,然后计算∠ACD的正弦值.
试题解析:(1)、作AH⊥BC于H 在Rt△ACH中,tan∠ACB=3,AC=![]() ,∴CH=1,AH=3
,∴CH=1,AH=3
在Rt△ABH中,∠B=45°,∴BH=AH=3 ∴S△ABC=![]() ×4×3=6
×4×3=6
(2)、作DE⊥AC于E,DF⊥BC于F S△ACD=×![]() ×DE=3,∴DE=
×DE=3,∴DE=![]()
在Rt△CDF中,CD=![]() ∴在Rt△CDE中,sin∠ACD=
∴在Rt△CDE中,sin∠ACD=![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
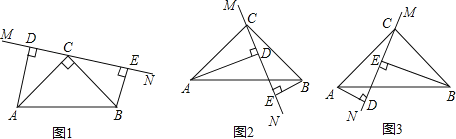
【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,
BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,请写出DE、AD、BE之间的等量关系并加以证明.
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE之间又有怎样的等量关系?请直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知识是用来为人类服务的,我们应该把它们用于有意义的方面.下面就两个情景请你作出评判.
情景一:从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?试用所学数学知识来说明这个问题.

情景二:A、B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由:

你赞同以上哪种做法?你认为应用数学知识为人类服务时应注意什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家电生产企业根据市场调查分析,决定调整产品生产方案,准备每周(按120个工时计算)生产空调、冰箱、彩电共360台,且彩电至少生产60台,已知生产这些家电产品每台所需工时和每台产值如下表:
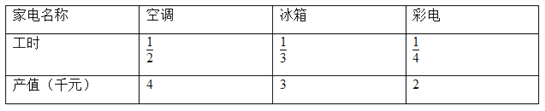
问每周应生产空调、冰箱、彩电各多少台,才能使产值最高?最高产值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
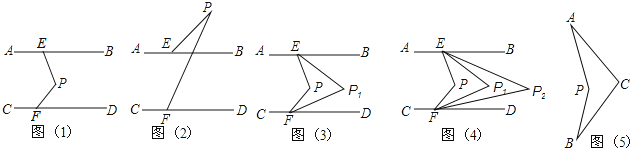
【题目】如图(1),直线AB∥CD,点P在两平行线之间,点E在AB上,点F在CD上,连结PE,PF.
(1)∠PEB,∠PFD,∠EPF满足的数量关系是 ,并说明理由.
(2)如图(2),若点P在直线AB上侧时,∠PEB,∠PFD,∠EPF满足的数量关系是 (不需说明理由)
(3)如图(3),在图(1)基础上,P![]() E平分∠PEB,P
E平分∠PEB,P![]() F平分∠PFD,若设∠PEB=x°,∠PFD=y°.则∠P
F平分∠PFD,若设∠PEB=x°,∠PFD=y°.则∠P![]() =______(用x,y的代数式表示),若P
=______(用x,y的代数式表示),若P![]() E平分∠P
E平分∠P![]() EB,P
EB,P![]() F平分∠P
F平分∠P![]() FD,可得∠P
FD,可得∠P![]() ,P
,P![]() E平分∠P
E平分∠P![]() EB,P
EB,P![]() F平分∠P
F平分∠P![]() FD,可得∠P
FD,可得∠P![]() …,依次平分下去,则∠P
…,依次平分下去,则∠P![]() =______.
=______.
(4)科技活动课上,雨轩同学制作了一个图(5)的“飞旋镖”,经测量发现∠PAC=28°,
∠PBC=30°,他很想知道∠APB与∠ACB的数量关系,你能告诉他吗?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com