
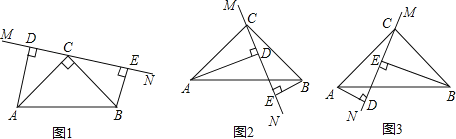
【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,
BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,请写出DE、AD、BE之间的等量关系并加以证明.
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE之间又有怎样的等量关系?请直接写出结论.
【答案】(1)证明见解析;(2)DE=AD-BE,证明见解析;(3)见解析.
【解析】(1)由已知AC=BC,∠ADC=∠CEB=90°,利用互余关系可证∠DAC=∠ECB,可证△ACD≌△CBE,得AD=CE,CD=BE,故AD+BE=CE+CD=DE;(2)此时,仍有△ACD≌△CBE,AD=CE,CD=BE,利用线段的和差关系得DE=AD-BE.
证明:(1)∵∠ADC=∠ACB=∠BEC=90°,
∴∠CAD+∠ACD=90°,∠BCE+∠CBE=90°,∠ACD+∠BCE=90°.
∴∠CAD=∠BCE.
∵AC=BC,
∴△ADC≌△CEB.
∴CE=AD,CD=BE.
∴DE=CE+CD=AD+BE.
(2)DE=AD﹣BE
证明:∵∠ADC=∠CEB=∠ACB=90°,
∴∠ACD=∠CBE.
又∵AC=BC,
∴△ACD≌△CBE.
∴CE=AD,CD=BE.
∴DE=CE﹣CD=AD﹣BE.
(3)DE=BE﹣AD(或AD=BE﹣DE,BE=AD+DE等).
易证得△ACD≌△CBE,
∴AD=CE,DC=BE,
∴DE=CD- CE =BE﹣AD.
“点睛”本题考查了用旋转法寻找证明三角形全等的条件,关键是利用全等三角形对应线段相等,将有关线段进行转化.


科目:初中数学 来源: 题型:
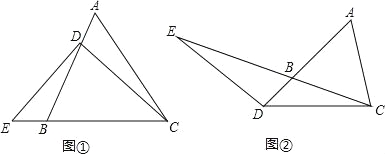
【题目】(2016山东省聊城市第29题)(1)、已知:△ABC是等腰三角形,其底边是BC,点D在线段AB上,E是直线BC上一点,且∠DEC=∠DCE,若∠A=60°(如图①).求证:EB=AD;
(2)、若将(1)中的“点D在线段AB上”改为“点D在线段AB的延长线上”,其它条件不变(如图②),(1)的结论是否成立,并说明理由;
(3)、若将(1)中的“若∠A=60°”改为“若∠A=90°”,其它条件不变,则![]() 的值是多少?(直接写出结论,不要求写解答过程)
的值是多少?(直接写出结论,不要求写解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明的袋子中装有形状、大小、质地完全相同的5个球,其中2个黑球、3个白球,从袋子中一次摸出3个球,下列事件是不可能事件的是( )
A. 摸出的是3个白球
B. 摸出的是3个黑球
C. 摸出的是2个白球、1个黑球
D. 摸出的是2个黑球、1个白球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的中线,E、F分别是AD和AD延长线上的点,DE=DF,连接BF、CE,下列说法:①CE=BF;②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.
其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016广东省梅州市第24题)(为方便答题,可在答题卡上画出你认为必要的图形)
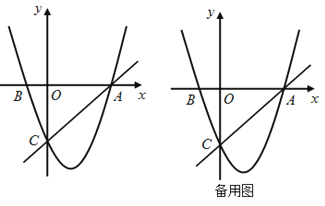
如图,在平面直角坐标系中,已知抛物线![]() 过A,B,C三点,点A的坐标是
过A,B,C三点,点A的坐标是![]() ,点C的坐标是
,点C的坐标是![]() ,动点P在抛物线上.
,动点P在抛物线上.
(1)b =_________,c =_________,点B的坐标为_____________;(直接填写结果)
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某招聘考试分笔试和面试两种,其中笔试按60%、面试按40%计算加权平均数,作为总成绩.孔明笔试成绩90分,面试成绩85分,那么孔明的总成绩是分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察如图所示的图形,写出下列问题的结果:

(1)这个图形的名称是 ;
(2)这个几何体有 个面,有 个底面,有 个侧面,底面是 形,侧面是 形.
(3)侧面的个数与底面多边形的边数有什么关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,AC=8 cm,CB=6 cm,点M、N分别是AC、BC的中点.
(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=a cm,其它条件不变,你能猜想MN的长度吗?并说明理由;
(3)若C在线段AB的延长线上,且满足AC﹣BC=bcm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由;
(4)你能用一句简洁的话,描述你发现的结论吗?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
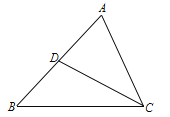
【题目】如图,在△ABC中,CD是AB边上的中线,已知∠B=45,tan∠ACB=3,AC=![]() ,
,
求:(1)△ABC的面积;(2)sin∠ACD的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com