
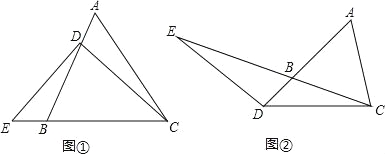
【题目】(2016山东省聊城市第29题)(1)、已知:△ABC是等腰三角形,其底边是BC,点D在线段AB上,E是直线BC上一点,且∠DEC=∠DCE,若∠A=60°(如图①).求证:EB=AD;
(2)、若将(1)中的“点D在线段AB上”改为“点D在线段AB的延长线上”,其它条件不变(如图②),(1)的结论是否成立,并说明理由;
(3)、若将(1)中的“若∠A=60°”改为“若∠A=90°”,其它条件不变,则![]() 的值是多少?(直接写出结论,不要求写解答过程)
的值是多少?(直接写出结论,不要求写解答过程)
【答案】(1)、证明过程见解析;(2)、成立;理由见解析;(3)、![]()
【解析】
试题分析:(1)、作DF∥BC交AC于F,由平行线的性质得出∠ADF=∠ABC,∠AFD=∠ACB,∠FDC=∠DCE,证明△ABC是等边三角形,得出∠ABC=∠ACB=60°,证出△ADF是等边三角形,∠DFC=120°,得出AD=DF,由已知条件得出∠FDC=∠DEC,ED=CD,由AAS证明△DBE≌△CFD,得出EB=DF,即可得出结论;(2)、作DF∥BC交AC的延长线于F,同(1)证出△DBE≌△CFD,得出EB=DF,即可得出结论; (3)、作DF∥BC交AC于F,同(1)得:△DBE≌△CFD,得出EB=DF,证出△ADF是等腰直角三角形,得出DF=![]() AD,即可得出结果.
AD,即可得出结果.
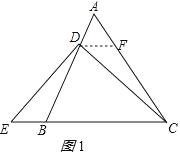
试题解析:(1)、作DF∥BC交AC于F,如图1所示:则∠ADF=∠ABC,∠AFD=∠ACB,∠FDC=∠DCE,
∵△ABC是等腰三角形,∠A=60°,∴△ABC是等边三角形,∴∠ABC=∠ACB=60°,
∴∠DBE=120°,∠ADF=∠AFD=60°=∠A,∴△ADF是等边三角形,∠DFC=120°, ∴AD=DF,
∵∠DEC=∠DCE, ∴∠FDC=∠DEC,ED=CD, ∴△DBE≌△CFD(AAS), ∴EB=DF, ∴EB=AD;
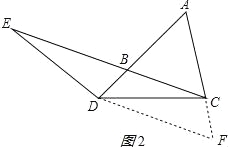
(2)、EB=AD成立;理由如下:作DF∥BC交AC的延长线于F,如图2所示:
同(1)得:AD=DF,∠FDC=∠ECD,∠FDC=∠DEC,ED=CD,又∵∠DBE=∠DFC=60°,∴△DBE≌△CFD(AAS),∴EB=DF, ∴EB=AD;
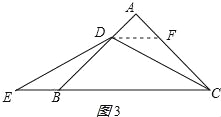
(3)、![]() ;理由如下:作DF∥BC交AC于F,如图3所示: 同(1)得:△DBE≌△CFD(AAS),
;理由如下:作DF∥BC交AC于F,如图3所示: 同(1)得:△DBE≌△CFD(AAS),
∴EB=DF,∵△ABC是等腰直角三角形,DF∥BC, ∴△ADF是等腰直角三角形, ∴DF=![]() AD,
AD,
∴![]() , ∴
, ∴![]() .
.


科目:初中数学 来源: 题型:
【题目】有一次同学聚会,他们的座位号是:小王的座位号与下列一组数中的负数的个数相等,小李的座位号与下列一组数中的正整数的个数相等,
6, ![]() ,0,200,
,0,200, ![]() ,5.22,0.01,+67,
,5.22,0.01,+67, ![]() ,10,300,24.
,10,300,24.
(1)试问小王、小李坐的各是第几号位置?
(2)若这次同学聚会的人数是小王的座位号的2倍与小李的座位号的4倍的和,请问这次聚会到了多少同学?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC与△BDE均为等边三角形,AB<BD,若△ABC不动,将△BDE绕点B旋转则在旋转过程中,AE与CD的大小关系为( )
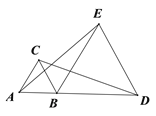
A. AE=CD B. AE>CD C. AE<CD D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市元宵节灯展参观人数约为470000,将这个数用科学记数法表示为( )
A. 4.7×106 B. 4.7×105 C. 0.47×106 D. 47×104
查看答案和解析>>
科目:初中数学 来源: 题型:
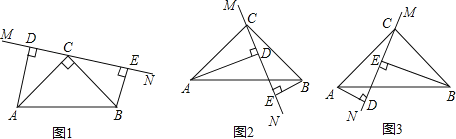
【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,
BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,请写出DE、AD、BE之间的等量关系并加以证明.
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE之间又有怎样的等量关系?请直接写出结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com